filmov
tv
Modified Logarithmic Sobolev Inequalities: ... (Lecture 3) by Prasad Tetali

Показать описание
PROGRAM: ADVANCES IN APPLIED PROBABILITY
ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava
DATE & TIME: 05 August 2019 to 17 August 2019
VENUE: Ramanujan Lecture Hall, ICTS Bangalore
Applied probability has seen a revolutionary growth in research activity, driven by the information age and exploding technological frontiers. Applications include the Internet and the world wide web, social networks, integrated supply chains in manufacturing networks, the highly intertwined international economies, and so on. The common thread running through these is that they are large interconnected systems that are emergent with very little top down design to optimize them. Probabilistic methods with limit theorems as their mainstay are best suited to find structure and regularity to help model, analyze and optimize such systems. Interface of probability with optimization and control, statistics, and machine learning has been the driving force behind the emerging paradigms, techniques and mathematics to address the huge scale of problems seen in such technological and commercial applications, not to mention several in biological or physical systems.
In this two-week program on advances in applied probability (PAAP), we will have some of the leading researchers in applied probability conduct short courses in emerging areas, including:
High dimensional computation
Inference, modelling and learning on networks
Limit theorems on random graphs, and
Monte Carlo methods.
There will be about ten short courses sprinkled with research talks each day. There will be research workshops on two of the days during the program.
During the program, Prof. Peter Glynn (Stanford University) will be delivering the Infosys - ICTS Turing lectures.
Eligibility Criteria:
Faculty and students working on Applied Probability or related area can apply. (Students should provide recommendation letters from their supervisors)
APPLICATION DEADLINE 15 June 2019
0:00:00 MODIFIED LOGARITHMIC SOBOLEV INEQUALITIES: THEORY, EXAMPLES AND CONSEQUENCES (LECTURE 3)
0:00:12 SUBGAUSSIAN AND TRANSPORT-ENTROPY
0:02:22 MASS TRANSPORT (MONGE-KANTORVICH)
0:03:46 ENTROPY INEQUALITY IMPLIES TRANSPORT INEQ.
0:05:12 PROOF (A LA OTTO-VILLANI)
0:08:58 LSI VERSUS MLSI
0:09:17 CONCENTRATION A LA HERBST
0:09:53 PROOF
0:10:19 PROOF (CONTD)
0:13:14 BOCHNER-BAKRY-EMERY CRITERION
0:17:23 BOCHNER-BAKRY-EMERY CRITERION (CONTD.)
0:20:18 MLSI AND BAKRY-EMERY CRITERION
0:28:32 BAKRY-EMERY, ... , SCHMUCKENSCHLAGER,...
0:31:06 GAMMA 2 CALCULUS
0:32:19 GAMMA 2 CALCULUS (CONTD.)
0:33:12 CHEEGER IS TIGHT IF CURVATURE
0:33:45 CD (K, ∞) WITH K 2 0: EXAMPLES
0:35:44 CHEEGER, CD(K, ∞) WITH K 0
0:39:26 (COARSE) RICCI OF HYPERCUBE
0:39:33 (COARSE) RICCI OF TRANSPOSITION GRAPH
0:40:03 PERES-TETALI "CONJECTURE"!
0:43:48 BASES-EXCHANGE WALK
0:45:04 MLSI FOR MATROID BASIS EXCHANGE
0:45:55 MANY OPEN PROBLEMS REMAIN!
0:46:07 STRONGLY LOG-CONCAVE POLYNOMIALS
0:48:39 STRONGLY LOG-CONCAVE DISTRIBUTIONS
0:49:24 ALTERNATIVE CHARACTERIZATION FOR SLC
0:52:02 THEOREM (CRYAN-GUO-MOUSA 2019)
0:52:29 LEVELS OF INDEPENDENT SETS
0:53:45 WEIGHTS FOR INDEPENDENT SETS
0:54:55 DIFFERENT VIEWS
0:56:42 RANDOM WALK BETWEEN LEVELS
0:57:15 DECOMPOSING THE WALKS
0:57:59 KEY LEMMA
0:58:24 BASE CASE
0:59:18 BOUND THE MIXING TIME DIRECTLY
0:59:28 FIN
ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava
DATE & TIME: 05 August 2019 to 17 August 2019
VENUE: Ramanujan Lecture Hall, ICTS Bangalore
Applied probability has seen a revolutionary growth in research activity, driven by the information age and exploding technological frontiers. Applications include the Internet and the world wide web, social networks, integrated supply chains in manufacturing networks, the highly intertwined international economies, and so on. The common thread running through these is that they are large interconnected systems that are emergent with very little top down design to optimize them. Probabilistic methods with limit theorems as their mainstay are best suited to find structure and regularity to help model, analyze and optimize such systems. Interface of probability with optimization and control, statistics, and machine learning has been the driving force behind the emerging paradigms, techniques and mathematics to address the huge scale of problems seen in such technological and commercial applications, not to mention several in biological or physical systems.
In this two-week program on advances in applied probability (PAAP), we will have some of the leading researchers in applied probability conduct short courses in emerging areas, including:
High dimensional computation
Inference, modelling and learning on networks
Limit theorems on random graphs, and
Monte Carlo methods.
There will be about ten short courses sprinkled with research talks each day. There will be research workshops on two of the days during the program.
During the program, Prof. Peter Glynn (Stanford University) will be delivering the Infosys - ICTS Turing lectures.
Eligibility Criteria:
Faculty and students working on Applied Probability or related area can apply. (Students should provide recommendation letters from their supervisors)
APPLICATION DEADLINE 15 June 2019
0:00:00 MODIFIED LOGARITHMIC SOBOLEV INEQUALITIES: THEORY, EXAMPLES AND CONSEQUENCES (LECTURE 3)
0:00:12 SUBGAUSSIAN AND TRANSPORT-ENTROPY
0:02:22 MASS TRANSPORT (MONGE-KANTORVICH)
0:03:46 ENTROPY INEQUALITY IMPLIES TRANSPORT INEQ.
0:05:12 PROOF (A LA OTTO-VILLANI)
0:08:58 LSI VERSUS MLSI
0:09:17 CONCENTRATION A LA HERBST
0:09:53 PROOF
0:10:19 PROOF (CONTD)
0:13:14 BOCHNER-BAKRY-EMERY CRITERION
0:17:23 BOCHNER-BAKRY-EMERY CRITERION (CONTD.)
0:20:18 MLSI AND BAKRY-EMERY CRITERION
0:28:32 BAKRY-EMERY, ... , SCHMUCKENSCHLAGER,...
0:31:06 GAMMA 2 CALCULUS
0:32:19 GAMMA 2 CALCULUS (CONTD.)
0:33:12 CHEEGER IS TIGHT IF CURVATURE
0:33:45 CD (K, ∞) WITH K 2 0: EXAMPLES
0:35:44 CHEEGER, CD(K, ∞) WITH K 0
0:39:26 (COARSE) RICCI OF HYPERCUBE
0:39:33 (COARSE) RICCI OF TRANSPOSITION GRAPH
0:40:03 PERES-TETALI "CONJECTURE"!
0:43:48 BASES-EXCHANGE WALK
0:45:04 MLSI FOR MATROID BASIS EXCHANGE
0:45:55 MANY OPEN PROBLEMS REMAIN!
0:46:07 STRONGLY LOG-CONCAVE POLYNOMIALS
0:48:39 STRONGLY LOG-CONCAVE DISTRIBUTIONS
0:49:24 ALTERNATIVE CHARACTERIZATION FOR SLC
0:52:02 THEOREM (CRYAN-GUO-MOUSA 2019)
0:52:29 LEVELS OF INDEPENDENT SETS
0:53:45 WEIGHTS FOR INDEPENDENT SETS
0:54:55 DIFFERENT VIEWS
0:56:42 RANDOM WALK BETWEEN LEVELS
0:57:15 DECOMPOSING THE WALKS
0:57:59 KEY LEMMA
0:58:24 BASE CASE
0:59:18 BOUND THE MIXING TIME DIRECTLY
0:59:28 FIN
 0:59:40
0:59:40
 1:00:20
1:00:20
 1:01:22
1:01:22
 0:57:57
0:57:57
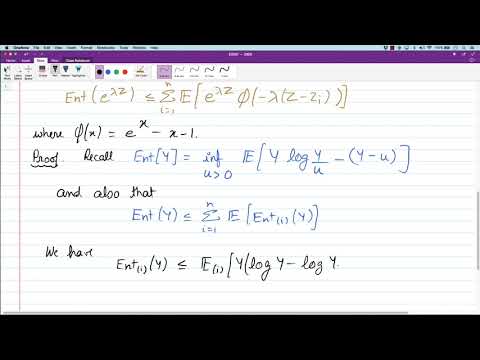 0:28:38
0:28:38
 0:21:26
0:21:26
 0:52:51
0:52:51
 0:35:51
0:35:51
 0:50:05
0:50:05
 0:17:16
0:17:16
 0:20:15
0:20:15
 0:42:53
0:42:53
 0:52:32
0:52:32
 0:40:29
0:40:29
 0:57:27
0:57:27
 0:23:31
0:23:31
 0:46:47
0:46:47
 0:49:49
0:49:49
 0:19:42
0:19:42
 0:48:50
0:48:50
 0:30:11
0:30:11
 0:11:45
0:11:45
 0:47:31
0:47:31
 0:22:22
0:22:22