filmov
tv
1W-MINDS: John Harlim, December 2, Diffusion maps on manifolds with boundaries for solving PDEs

Показать описание
I will discuss recent efforts in using the Diffusion Maps (DM) algorithm to solve elliptic PDEs on unknown manifolds using point clouds data. The key idea rests on the fact that away from the boundary, the second-order elliptic differential operators can be approximated by integral operators defined with appropriate Gaussian kernels. On manifolds with boundary, however, such an approximation is only valid for functions that satisfy the Neumann boundary condition. Motivated by the classical ghost-point correction in the finite-difference method for solving Neumann problems, we extend the diffusion maps algorithm with ghost points such that it is a consistent estimator in the pointwise sense even near the boundary. Applying the proposed algorithm, which we called the Ghost Points Diffusion Maps (GPDM), to solve the well-posed elliptic PDEs with Dirichlet, Neumann, or Robin boundary conditions, we establish the convergence of the approximate solution under appropriate smoothness assumptions. I will also discuss a neural-network regression solution on an algebraic equation induced by the DM/GPDM discretization. In addition to theoretical convergence for a wide enough neural network model, we numerically found that the proposed solver avoids the classical large matrix inversion problem. I will also discuss the application of DM/GPDM on Bayesian elliptic inverse problems. If time permits, I will also present symmetric Graph-Laplacian matrices that spectrally converge to the Laplace-Beltrami operator defined on compact manifolds with homogeneous Neumann and Dirichlet boundary conditions.
 0:59:13
0:59:13
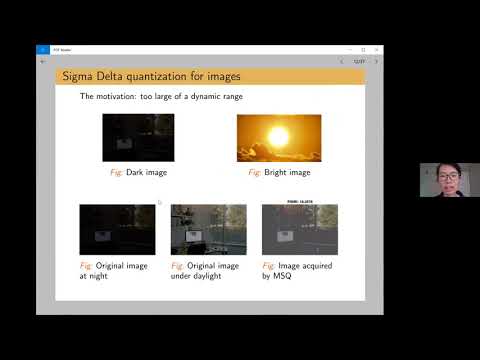 0:42:51
0:42:51
 1:45:44
1:45:44
 0:58:10
0:58:10
 0:04:35
0:04:35
 1:09:34
1:09:34
 0:08:04
0:08:04
 0:04:20
0:04:20
 0:04:58
0:04:58
 0:03:01
0:03:01
 0:32:14
0:32:14
 0:56:59
0:56:59
 0:45:36
0:45:36
 0:23:40
0:23:40
 0:35:38
0:35:38
 0:54:10
0:54:10
 1:11:31
1:11:31
 2:19:01
2:19:01
 0:36:13
0:36:13
 0:27:07
0:27:07
 0:45:52
0:45:52
 1:39:59
1:39:59
 0:59:02
0:59:02
 0:42:27
0:42:27