Differential Equations Final Exam Review Problems and Solutions (includes Laplace Transforms)

1) First-order Laplace transform problem with unit step function. 2) Prove a simple saddle point is unstable. 3) Trapping region in polar coordinates and Poincare-Bendixson theorem. 4) Negative of potential function for a gradient system is a Lyapunov function. 5) Hamiltonian system. 6) Second-order Laplace transform problem. 7) Nonlinear bifurcation problem (use the Jacobian matrix and trace-determinant plane). 8) Stable equilibrium point. 9) Hyperbolic equilibrium point. 10) Sensitive dependence on initial conditions. 11) Partial differential equation (heat equation PDE).

Links and resources
===============================

⏱️TIMESTAMPS⏱️
(0:00) Video topics
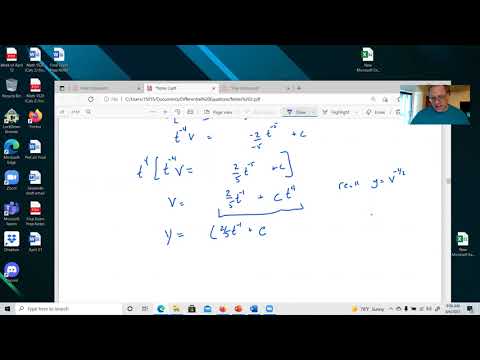
(0:24) 1st Order Laplace transform with discontinuous forcing problem (unit step function (Heaviside function) with jump discontinuity at t = 4.
(10:47) Prove a saddle point is unstable
(18:35) Trapping region and the Poincare-Bendixson Theorem (polar coordinates are helpful)
(25:26) Function -G is a Lyapunov function of the gradient system corresponding to the potential function G.
(28:48) Hamiltonian system with a degenerate (non-hyperbolic) equilibrium point at the origin (a strange type of saddle point).
(37:48) 2nd Order Laplace transform problem
(49:00) Nonlinear bifurcation problem (a one parameter family of nonlinear systems). Linearization with the Jacobian matrix is used.
(1:02:27) Is a center a stable equilibrium point?
(1:03:53) Hyperbolic equilibrium point
(1:05:25) Sensitive dependence on initial conditions (butterfly effect or "chaos")
(1:06:07) Heat equation PDE example solution (partial differential equation)

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.

[colejhudson]

Bill this is exceptional! For all of the educational content on YouTube, very little of it gets into the nitty gritty details by actually solving problems to completion. Thoroughly appreciate you recording this one and all the others.