Длина параболы и спирали Архимеда: что у них общего?

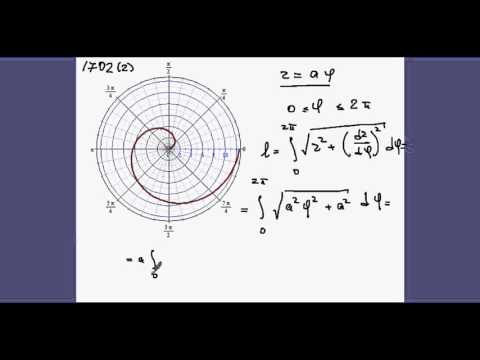
В этом видео получим формулы для длины дуги кривой, заданной в параметрическом и в явном виде, а так же в полярной системе координат. А для примера найдем длину параболы и спирали Архимеда и выясним что у них вообще может быть общего и получим несколько интересных свойств.

Если у вас есть возможность, поддержите канал:
сбербанк: 4276160020048840
тинькофф: 5536914075973911

[AlexeyEvpalov]

Всё подробно с наглядными иллюстрациями. Спасибо за познавательную лекцию.

[vadimgerasimenko]

Досмотрел "до этого момента". Понравилось) Спасибо за ваш труд

[твопапа]

Кайф, спасибо большое за уравнение длинны кривой

[igorsoftvariant]

Второй раз посмотрел, показалось ещё интереснее. Вообще канал отличный, таких больше нет

[vladmar]

Интересно девки пляшут, я о таком даже не подозревал. Спасибо за видео.

[HerrHoldem]

Большое спасибо за видео! Факт действительно занимательный.
У вас талант к повествованию: я сначала думал пропустить часть с выведением формул (так как и сам это знаю), но интерес к вашему рассказу не позволил мне это сделать.

Желаю вам успехов, видео очень крутые!

[arts]

Вы не перестаёте меня удивлять. Я только недавно познакомился с Вашим каналом, но уже успел понять, что у Вас очень качественные видео. Мне очень нравится, что Вы детально разъясняете каждое действие и подаёте все с доказательствами. К тому же темы Ваших видео безумно интересные и в полной мере демонстрируют насколько красивой может быть математика. Я очень благодарен Вам за Ваш труд 👍

[VSU_vitebsk]

хорошая занимательная лекция! Отдельный плюс за наглядность

[_]

Поступил на первый курс. Ролики стал смотреть с ещё большим интересом, спасибо Вам!

[KalininEvgen]

Ну я человек простой: вижу новое видео -- ставлю лайк!
3:35 то чувство, когда по сути выводишь формулу длины траектории через время и скорость))
А вообще видео очень интересное! Даже со своим уровнем знания удивляюсь тому, что можно усмотреть в, казалось бы, простых вещах)

[kvach]

Те самые математические штучки, которые вылезают тут и там. И всегда говоришь себе, ну точно запомню, а потом, когда встретится, я сразу их пущу в ход. Но опыт говорит, что через три дня ужже пусто )) Да я сумму синусов через матрицу поворота или через умножение комплексных чисел каждый раз вспоминаю. ))

[nazimavaleeva]

Завтра досмотрю, спасибо все очень хорошо объяснили

[vintik]

Привет. Сейчас в вузе проходим конические сечения (кривые второго порядка), если есть возможность - можешь в следующих видео рассказать о них (общее уравнение в плоскости, в которой лежат, то есть его вывод из того факта, что это сечение конуса; эксцентриситет, диаметры и сопряжённые диаметры, директриса)

[kvach]

Длина дуги постоянного радиуса r равна rdϕ. Изменение вектора равно dr. По теореме пифагора длина квадрата дуги кривой будет (dr)^2+(rdϕ)^2. Если взять квадратный корень и вынести дифференциал угла за скобку, то получится оно )) Каждый раз так высчитывать метрический тензор целиком — глаз выпадет )) Я лично в таких скобках по три раза лажану.

[Serghey_]

Знаете, как дорожники измеряют ширину дорожного полотна? Не линейкой а прокатывают колёсико с известной длиной окружности по заданному отрезку. Число оборотов умножаем на длину обода колёсика и получаем измеряемый отрезок или длину гладкой кривой, вдоль которой прокатываем колёсико.

[fskvirelloff]

пришлось тут как-то решать обратную задачу. Есть лента некоего материала, известной толщины. Эта лента плотно наматывается на вал известного диаметра. Вопрос : какого диаметра будет получившийся рулон ? То есть, то что лента сворачивается в спираль я понял сразу. Дальше я подумал, что длины витков этой спирали образуют прогрессию... короче и так и этак, ничего не получается. Точный ответ от меня не требовался, чай не в америку стрелять, обошлись приближенно, плюс-минус наугад. А вот после этого видео, вспомнил тот эпизод и задумался...

[jabahuyaba]

Приятно вспомнить теорию перед задачей. Но разве нужно брать больше хорд? Не правильней ли будет сказать, что нужно уменьшать размер большей из хорд?

[nurlybekmoldagaliev]

2:29 не забудьте что если выполнятся равенство ∆L=∆t для любого t, то длина дуги будет равна t(B)-t(A).

[staf]

14:27 где-то этот интеграл попадался часто в матанализе

[andreiantonov]

9:06 ну как бы очевидно что это свойство не только параболы, а любой функции, у которой производная стремится к бесконечности с ростом x.