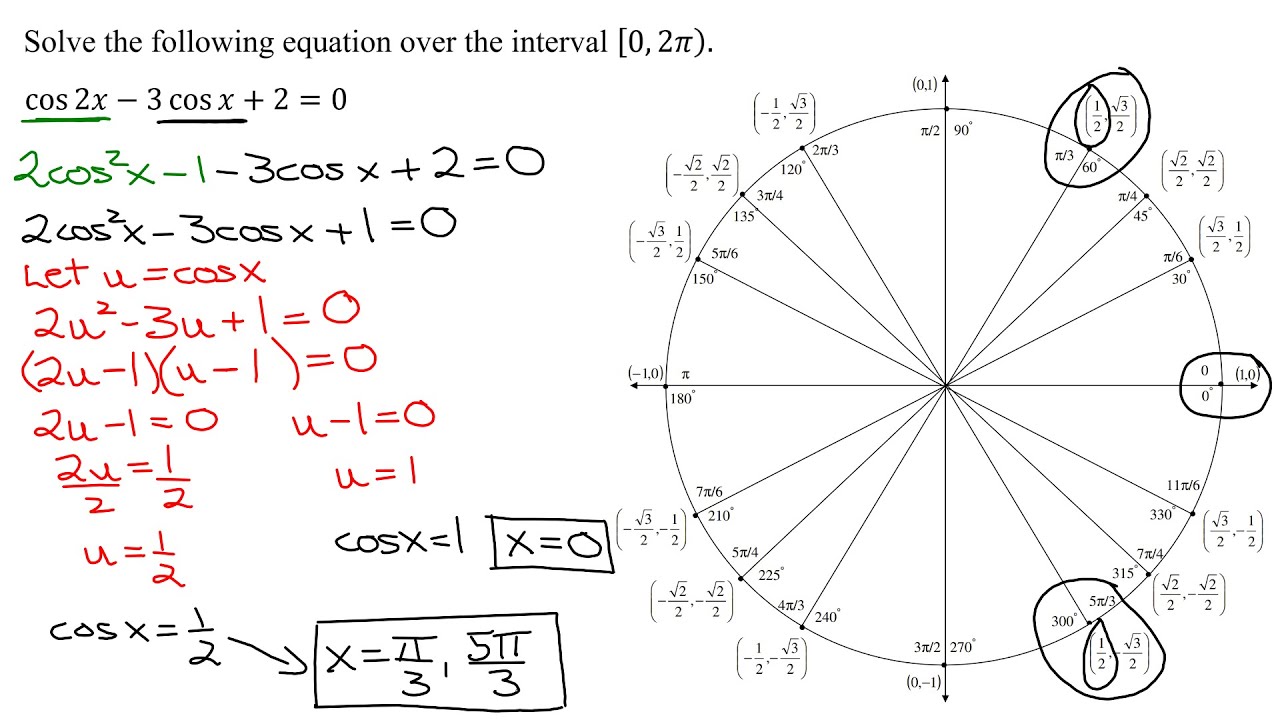
Solve, in Radians, the Trig Equation cos(2x)-3cos(x)+2=0 That Leads To Quadratic Equation in Cos(x)

Показать описание

The trigonometric equation to be solved is cos(2x)-3cos(x)+2=0. As the equation contains cos(2x) and cos(x), the identity for cos(2x) needs to be used. As the equation also contains cos(x) the version of cos(2x) used is the one that only contains the cosine of x: cos(2x)=2cos^2(x)-1. When this is substituted into the given equation, a quadratic equation in cos(x) is obtained. This is then factored and each factor is set equal to zero. The 2 simple linear equations are solved and exact solutions are found in radians using the unit circle.

Timestamps
0:00 Introduction
0:52 Use cos(2x)=2cos^2(x)-1
3:00 Factor Quadratic Equation in cos(x)
4:20 Set Each Factor = 0
5:30 Use Unit Circle