filmov
tv
Container with Most Water - Leetcode 11 - Python
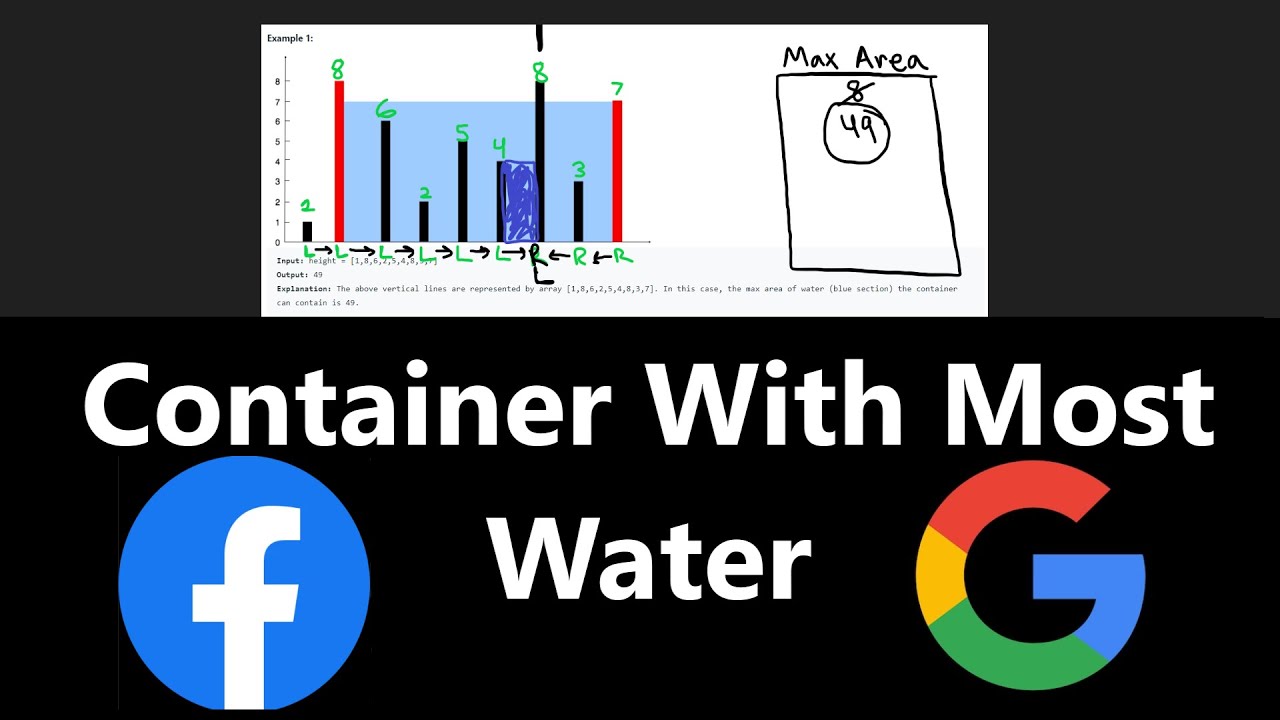
Показать описание
0:00 - Brute Force
5:25 - Optimal Solution
9:30 - Coding Optimal Solution
Leetcode 11
#CodingInterview #leetcode #neetcode
Disclosure: Some of the links above may be affiliate links, from which I may earn a small commission.
Container with Most Water - Leetcode 11 - Python
Container With Most Water - Leetcode 11 - 2 Pointers (Python)
Amazon LOVES This Coding Question! | Container With Most Water - Leetcode 11
LeetCode Container With Most Water Explained - Java
Container with most water | Leetcode #11
Container With Most Water | Live Coding with Explanation | Leetcode - 11
Container With Most Water - LeetCode 11 - Python
11. Container With Most Water || LEETCODE || code + intuition
LeetCode 11: Container With Most Water (Medium)
LeetCode #11: Container With Most Water
CONTAINER WITH MOST WATER | LEETCODE # 11 | PYTHON 2 POINTERS SOLUTION
Container With Most Water - (Meta, Google, Amazon) : Explanation ➕ Live Coding 🧑🏻💻👩🏻💻...
Container with Most Water Problem | Brute & Optimal Solution | Two Pointer Approach - Leetcode 1...
Container With Maximum Water (LeetCode 11) | Full Solution with Visuals | Study Algorithms
Container With Most Water - LeetCode 11 - Java
DSA Phir se with Sumeet | Leetcode 11 | Container with most water
Amazon Interview Question - Container With Most Water
Container With Most Water
Container With Most Water - LeetCode 11 - JavaScript
Container with most water problem - Inside code
Container With Most Water || LeetCode 11 || C++
11. Container With Most Water
Container With Most Water | Detailed Explanation | LeetCode Solution | Geekific
Container With Most Water - LeetCode 11
Комментарии
 0:12:37
0:12:37
 0:06:48
0:06:48
 0:00:58
0:00:58
 0:05:40
0:05:40
 0:12:33
0:12:33
 0:04:58
0:04:58
 0:08:44
0:08:44
 0:08:01
0:08:01
 0:19:35
0:19:35
 0:07:07
0:07:07
 0:11:11
0:11:11
 0:18:38
0:18:38
 0:32:00
0:32:00
 0:12:42
0:12:42
 0:15:21
0:15:21
 0:15:08
0:15:08
 0:00:58
0:00:58
 0:01:08
0:01:08
 0:05:50
0:05:50
 0:05:50
0:05:50
 0:09:28
0:09:28
 0:09:06
0:09:06
 0:03:57
0:03:57
 0:02:55
0:02:55