filmov
tv
Fatou's Lemma Made Simple :Intuitive Understanding and Applications

Показать описание
The Fatou's Lemma is a fundamental result in measure theory that provides a lower bound for the integral of the limit of a sequence of non-negative measurable functions. In this video, we will start by explaining what measure theory is and why it is important. We will then introduce the Fatou's Lemma and explain its statement and proof.
To make the concept of measure theory more accessible, we will use real-world examples to illustrate how it is used in various fields such as physics, economics, and engineering. We will also provide a brief overview of other important concepts in measure theory, such as the Monotone Convergence Theorem and the Dominated Convergence Theorem.
After introducing the Fatou's Lemma, we will provide a step-by-step example of how it can be applied to a sequence of non-negative measurable functions. We will use clear visuals and concise explanations to make the example easy to follow.
Throughout the video, we will also provide additional tips and insights for viewers who want to learn more about measure theory or pursue further studies in the field. We will highlight common mistakes and misconceptions and provide resources for additional learning.
By the end of the video, you will have a solid understanding of the Fatou's Lemma and its importance in measure theory. You will also have a deeper appreciation for the role of measure theory in various fields and the power of mathematical abstraction to solve real-world problems.
.....................................................................
Please Subscribe!
....................................................................
Possible answered questions :
What is Fatou's lemma?
What is the statement of Fatou's lemma?
How is Fatou's lemma used in real analysis?
What are the conditions required for Fatou's lemma to hold?
What is the significance of Fatou's lemma in measure theory?
Can Fatou's lemma be applied to non-negative sequences of functions?
Can Fatou's lemma be extended to general measures?
What is the difference between Fatou's lemma and dominated convergence theorem?
How does Fatou's lemma relate to the monotone convergence theorem?
Can Fatou's lemma be used to prove the Lebesgue's dominated convergence theorem?
What are some applications of Fatou's lemma in probability theory?
Can Fatou's lemma be used to prove the convergence of a sequence of random variables?
What are some examples of the application of Fatou's lemma in mathematical physics?
Can Fatou's lemma be used to prove the ergodic theorem?
How does Fatou's lemma relate to the concept of liminf and limsup?
To make the concept of measure theory more accessible, we will use real-world examples to illustrate how it is used in various fields such as physics, economics, and engineering. We will also provide a brief overview of other important concepts in measure theory, such as the Monotone Convergence Theorem and the Dominated Convergence Theorem.
After introducing the Fatou's Lemma, we will provide a step-by-step example of how it can be applied to a sequence of non-negative measurable functions. We will use clear visuals and concise explanations to make the example easy to follow.
Throughout the video, we will also provide additional tips and insights for viewers who want to learn more about measure theory or pursue further studies in the field. We will highlight common mistakes and misconceptions and provide resources for additional learning.
By the end of the video, you will have a solid understanding of the Fatou's Lemma and its importance in measure theory. You will also have a deeper appreciation for the role of measure theory in various fields and the power of mathematical abstraction to solve real-world problems.
.....................................................................
Please Subscribe!
....................................................................
Possible answered questions :
What is Fatou's lemma?
What is the statement of Fatou's lemma?
How is Fatou's lemma used in real analysis?
What are the conditions required for Fatou's lemma to hold?
What is the significance of Fatou's lemma in measure theory?
Can Fatou's lemma be applied to non-negative sequences of functions?
Can Fatou's lemma be extended to general measures?
What is the difference between Fatou's lemma and dominated convergence theorem?
How does Fatou's lemma relate to the monotone convergence theorem?
Can Fatou's lemma be used to prove the Lebesgue's dominated convergence theorem?
What are some applications of Fatou's lemma in probability theory?
Can Fatou's lemma be used to prove the convergence of a sequence of random variables?
What are some examples of the application of Fatou's lemma in mathematical physics?
Can Fatou's lemma be used to prove the ergodic theorem?
How does Fatou's lemma relate to the concept of liminf and limsup?
Комментарии
 0:07:36
0:07:36
 1:27:33
1:27:33
 0:21:02
0:21:02
 0:05:13
0:05:13
 0:05:22
0:05:22
 0:23:44
0:23:44
 0:05:31
0:05:31
 0:54:05
0:54:05
 0:08:05
0:08:05
 0:18:17
0:18:17
 0:49:23
0:49:23
 0:31:41
0:31:41
 0:21:02
0:21:02
 0:36:58
0:36:58
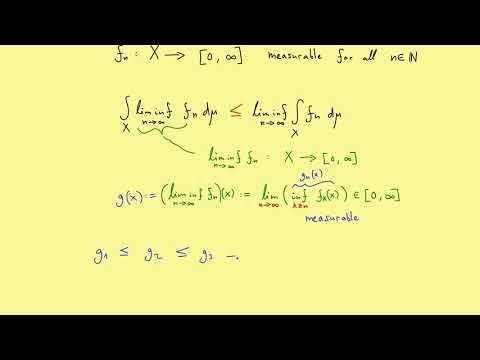 0:08:25
0:08:25
 0:04:18
0:04:18
 0:07:23
0:07:23
 0:22:45
0:22:45
 0:08:50
0:08:50
 0:08:37
0:08:37
 0:08:14
0:08:14
 0:59:29
0:59:29
 0:33:04
0:33:04
 0:29:55
0:29:55