filmov
tv
One of the coolest integrals ever ! and we're gonna solve it using Feynman integration

Показать описание
One of my favourite integrals!
Remember to like and subscribe for more cool math and physics videos.
Remember to like and subscribe for more cool math and physics videos.
One of the coolest integrals ever ! and we're gonna solve it using Feynman integration
ONE OF THE COOLEST INTEGRALS EVER!! int (0,1) ln(x)/sqrt(x(1-x^2))
Feynman's technique is the greatest integration method of all time
Feynman's Technique: This is the greatest integration method of All Time
how to solve these HARD integrals
How to do two (or more) integrals with just one
i did another 100 integrals!
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
The coolest way to evaluate the Fresnel integrals (Feynman's technique)
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Integration (Calculus)
Researchers thought this was a bug (Borwein integrals)
Type 1 improper integrals! calculus 2
One Spicy Class of Integrals.
Feynman's Technique of Integration
integration by parts, DI method, VERY EASY
You're gonna love this satisfying integration problem (integral from zero to infinity of 1/(x^4...
A beautiful result in calculus: Solution using Feynman integration ( Integral cos(x)/(x^2+1) )
100 integrals (world record?)
Calculus 1 - Integration & Antiderivatives
Integrals: degree of top GREATER than bottom. #calculus #integrals #mathchallenge #mathtricks
Integration Tricks (That Teachers Won't Tell You) for Integral Calculus
Understand u substitution for integration (3 slightly trickier examples), calculus 1 tutorial
Advanced Strategy for Integration in Calculus
Комментарии
 0:13:33
0:13:33
 0:15:38
0:15:38
 0:12:13
0:12:13
 0:01:07
0:01:07
 0:09:45
0:09:45
 0:18:03
0:18:03
 0:00:16
0:00:16
 0:20:46
0:20:46
 0:21:41
0:21:41
 0:22:40
0:22:40
 0:07:04
0:07:04
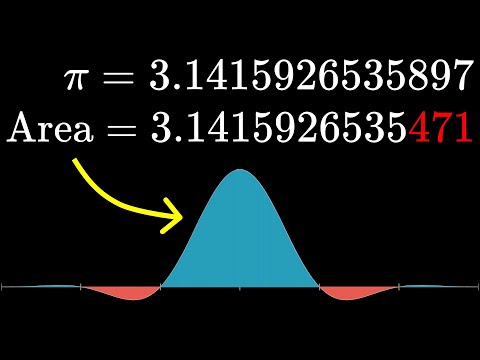 0:17:26
0:17:26
 0:27:48
0:27:48
 0:12:06
0:12:06
 0:10:02
0:10:02
 0:16:59
0:16:59
 0:08:33
0:08:33
 0:12:18
0:12:18
 5:50:23
5:50:23
 0:40:04
0:40:04
 0:00:48
0:00:48
 0:11:26
0:11:26
 0:14:41
0:14:41
 0:16:13
0:16:13