filmov
tv
What is General Relativity? Lesson 6: Introduction to compact coordinates
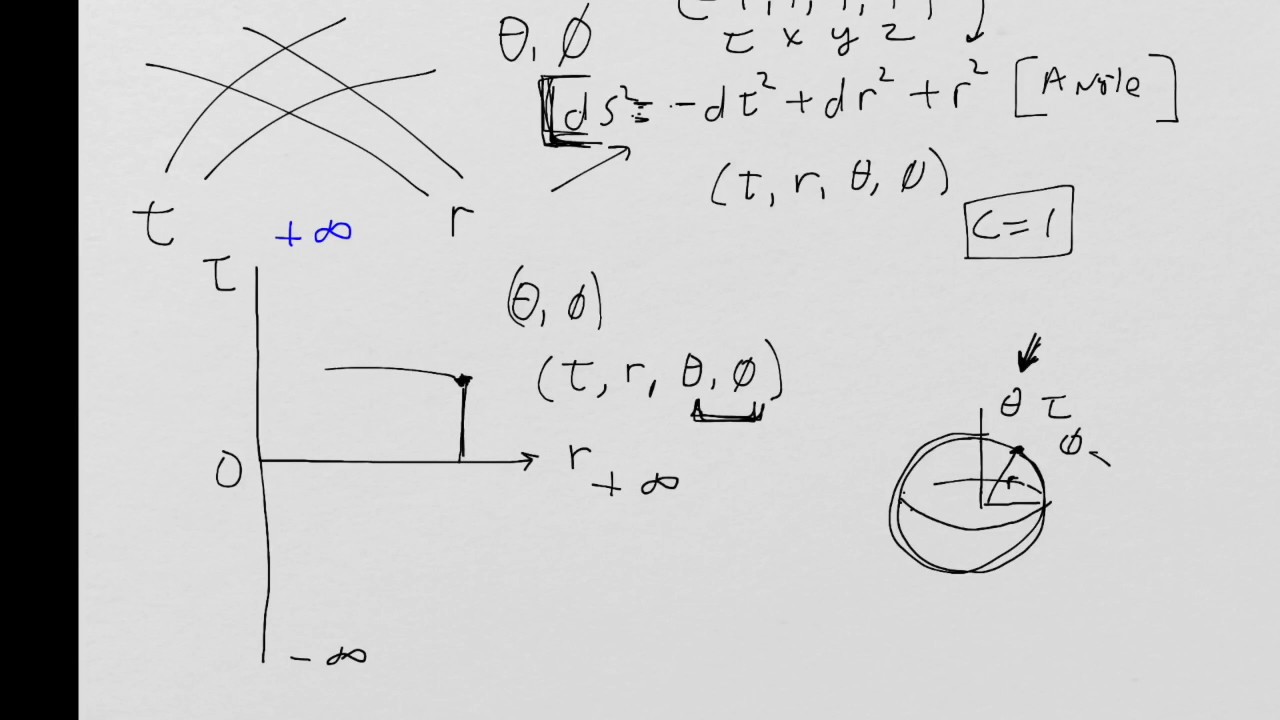
Показать описание
This video is about What is General Relativity? Lesson 6: Introduction to compact coordinates
General Relativity Explained simply & visually
What is General Relativity Lesson 1: Prerequisites, Books, Units, and Syllabus
What is General Relativity? Lesson 36: Introduction to the Einstein Equation
General Relativity Lecture 1
General Relativity: The Curvature of Spacetime
What is General Relativity? Lesson 0 and Lesson 75: Invitation and Recap
Simple Relativity - Understanding Einstein's Special Theory of Relativity
What is General Relativity? Lesson 37: The line element
The Mind-Bending Science of Einstein's Relativity
Gravity Visualized
What is General Relativity?
Relativity 107f: General Relativity Basics - Einstein Field Equation Derivation (w/ sign convention)
What is General Relativity? Lesson 69: The Einstein Equation
Lesson 24 - Lecture 1 - General Relativity - OpenStax
What is General Relativity? Lesson 71: Newton's Force Law from General Relativity
What is General Relativity? Lesson 39: The curvature - formal introduction
What is General Relativity? Lesson 41: The Commutator in Flat Space
What is General Relativity? Lesson 68: The Einstein Tensor
What is General Relativity? Lesson 26: The central force problem in classical mechanics
What is General Relativity? Lesson 52: Scalar Curvature Part I
Time Dilation - Einstein's Theory Of Relativity Explained!
Particle Physicist Takes General Relativity #shorts
What is General Relativity? Lesson 4: Introduction to the Connection
What is General Relativity? Lesson 16: The metric connection
Комментарии
 0:14:04
0:14:04
 0:45:59
0:45:59
 0:21:13
0:21:13
 1:49:28
1:49:28
 0:06:20
0:06:20
 0:38:38
0:38:38
 0:05:56
0:05:56
 0:48:40
0:48:40
 0:00:56
0:00:56
 0:09:58
0:09:58
 0:13:43
0:13:43
 0:36:51
0:36:51
 0:54:01
0:54:01
 0:19:36
0:19:36
 0:15:50
0:15:50
 0:46:07
0:46:07
 0:36:44
0:36:44
 0:46:56
0:46:56
 0:54:59
0:54:59
 0:47:55
0:47:55
 0:08:06
0:08:06
 0:00:10
0:00:10
 1:02:33
1:02:33
 0:55:39
0:55:39