filmov
tv
C++ STL -- Binary Search (std::binary_search, std::lower_bound, std::upper_bound)
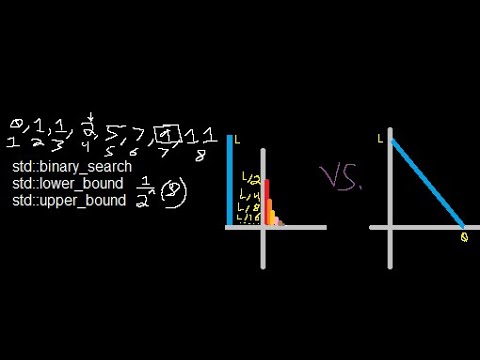
Показать описание
In this video I give a brief explanation of how a binary search is implemented and what kind of data it works with (contiguously iterable and sorted in ascending order).
After my visual introduction, I write some code that shows how to use std::binary_search, std::lower_bound, and std::upper_bound in order to determine whether a specific element exists and, if so, how to find its location in memory (or an iterator that references it). I give a practical example of keeping a vector's elements sorted while adding new elements into it -- and of keeping a vector full of sorted and unique elements.
For anyone who cares, the worst-case time complexity should be O(log2(element count)) because we skip half of the remaining elements, each step. This is like skipping through the elements at a rate of element_count / 2^n, where n begins at 1 and increases by 1, each check. We skip fewer elements, each time, but already cut out 50% of them in the first check. This is like [(.5+.25+.125+.0625...+0)*element_count] skipped elements, but with the sequence possibly ending early, if/when the desired value is located.
If we start with a set of length N, how many divisions of two does it take to reach 0 (presuming truncation, each step)?
Example with set of 11 elements:
[11] ->5->2->1->0
log2(11) = 3.4594316186372972561993630467258
4 steps ( ceil ( 3.4 ) = 4 )
Example with 27 elements:
[27]->13->6->3->1->0
log2(27) = 4.75488750216
5 steps ( ceil ( 4.7 ) = 5 )
This is basically asking to solve 2^x = N;
Thus, log2(2^x) = log2(N) --> x = log2 ( N )
In reality, it's x = ceil(log2(N)), in the worst case.
As always, I hope that you've found the video useful and/or entertaining. If you have any questions, suggestions, criticisms, or other thoughts, please feel encouraged to post a comment. Your feedback helps me to improve this content for everyone who's interested in watching -- and it can help me to improve my own understanding/approach to solving problems.
Thank you for watching. Have a great day!
After my visual introduction, I write some code that shows how to use std::binary_search, std::lower_bound, and std::upper_bound in order to determine whether a specific element exists and, if so, how to find its location in memory (or an iterator that references it). I give a practical example of keeping a vector's elements sorted while adding new elements into it -- and of keeping a vector full of sorted and unique elements.
For anyone who cares, the worst-case time complexity should be O(log2(element count)) because we skip half of the remaining elements, each step. This is like skipping through the elements at a rate of element_count / 2^n, where n begins at 1 and increases by 1, each check. We skip fewer elements, each time, but already cut out 50% of them in the first check. This is like [(.5+.25+.125+.0625...+0)*element_count] skipped elements, but with the sequence possibly ending early, if/when the desired value is located.
If we start with a set of length N, how many divisions of two does it take to reach 0 (presuming truncation, each step)?
Example with set of 11 elements:
[11] ->5->2->1->0
log2(11) = 3.4594316186372972561993630467258
4 steps ( ceil ( 3.4 ) = 4 )
Example with 27 elements:
[27]->13->6->3->1->0
log2(27) = 4.75488750216
5 steps ( ceil ( 4.7 ) = 5 )
This is basically asking to solve 2^x = N;
Thus, log2(2^x) = log2(N) --> x = log2 ( N )
In reality, it's x = ceil(log2(N)), in the worst case.
As always, I hope that you've found the video useful and/or entertaining. If you have any questions, suggestions, criticisms, or other thoughts, please feel encouraged to post a comment. Your feedback helps me to improve this content for everyone who's interested in watching -- and it can help me to improve my own understanding/approach to solving problems.
Thank you for watching. Have a great day!
 0:12:58
0:12:58
 0:03:22
0:03:22
 0:10:24
0:10:24
 0:07:54
0:07:54
 0:05:34
0:05:34
 0:15:33
0:15:33
 0:14:49
0:14:49
 0:03:01
0:03:01
 0:18:39
0:18:39
 0:02:04
0:02:04
 1:11:42
1:11:42
 0:10:31
0:10:31
 0:13:29
0:13:29
 0:03:52
0:03:52
 0:09:02
0:09:02
![#031 [Data Structures]](https://i.ytimg.com/vi/qxhfkoDGGZc/hqdefault.jpg) 0:15:11
0:15:11
 0:32:26
0:32:26
 0:51:12
0:51:12
 0:10:11
0:10:11
 0:12:50
0:12:50
 0:34:42
0:34:42
 0:11:46
0:11:46
 0:06:44
0:06:44