Evaluate `lim_(xto0){(sqrt(1+x)-sqrt(1-x))/(x)}.`

Показать описание

Doubtnut

Рекомендации по теме

Комментарии

...Good day, An alternative way to solve the same indeterminate limit is as follows: lim(x-->0){(sqrt(1 + x) - sqrt(1 - x))/x} (multiply numerator and denominator by 2) = lim(x-->0){2(sqrt(1 + x) - sqrt(1 - x))/2x)} (rewrite denominator 2x as follows: 2x = (1 + x) - (1 - x)) = lim(x-->0){2(sqrt(1 + x) - sqrt(1 - x))/((1 + x) - (1 - x))} (treat denominator as a difference of squares: (1 + x) - (1 - x) = (sqrt(1 + x) - sqrt(1 - x))(sqrt(1 + x) + sqrt(1 - x)), and then cancel the factor (sqrt(1 + x) - sqrt(1 - x)) of numerator and denominator) = lim(x-->0){2/(sqrt(1 + x) + sqrt(1 - x))} (evaluate the solvable limit) = 2/(sqrt(1) + sqrt(1)) = 2/2 = 1... I hope you appreciate this method too, Thank you for your math efforts, and take care, Jan-W

jan-willemreens

Evaluate `lim_(xto0){(sqrt(1+x)-sqrt(1-x))/(x)}.`

Evaluate `lim_(xto0){(sqrt(1+x)-sqrt(1-x))/(x)}.`

Evaluate `lim_(x- gt0) {(sqrt(1+x) - sqrt(1-x))/x}`

`lim_(x to 0)((x)/(sqrt(1+x)-sqrt(1-x)))` is equal to

Evaluate `underset(x to 0)(lim) (sqrt(1 + x) + sqrt(1 - x))/(1 - x)`

Evaluate : lim_(xrarr0) (sqrt(1+x)-sqrt(1-x))/( x) | 11 | LIMITS AND DERIVATIVES | MATHS | NAGE...

Evaluate the following limits: `lim_(xto0)((sqrt(1+x^(2))-sqrt(1+x))/(sqrt(1+x^(3))-sqrt(1+x)))`

What is `underset(xto0)lim(sqrt(1+x-1))/(x)`

Limit of (sqrt(1 - x^2) - 1)/x using L'hopitals Rule

`lim_(xto0)(sinx)/(sqrt(x+1)-sqrt(1-x))` is equal to

Limit as x goes to 0 of x/[1-sqrt(1-x)]

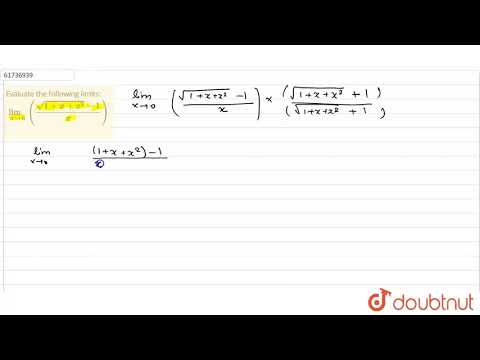
Evaluate the following limits: `lim_(xto0)((sqrt(1+x+x^(2))-1)/(x))`

Evaluate `lim_(xto0)((sqrt(1+3x)-sqrt(1-3x)))/(x).`

`lim_(xto0)(sqrt(1+x)-sqrt(1-x))/(sin^(-1)x)`

Calculus Help: Find the limit - Lim {x approaches to 0} ( sqrt(x) - 1 ) / ( x - 1 ) - Basic Formula

CBSE Class 12 Boards Maths Evaluate: `l i m xvecoo\ ((sqrt(1+x)\ -\ sqrt(1-x))/(sin^(-1)x))`

limit (x³-1)/(sqrt(x) - 1) as x approaches 1

Evaluate : lim (x→0) (√(1 + 3x) - √(1 - 3x))/x

Evaluate the following limits: `lim_(xto0)(sqrt(1+sinx)-1sqrt(1-sinx))/(x)`

lim (1+x) ^1/x as x tends to 0 , #Easy #short # Trick

`lim_(x- gt0) x/(sqrt(1+x)-sqrt(1-x))`

Limit (sqrt(x) - x²)/(1-sqrt(x)), (sqrt(6-x)-2)/(sqrt(3-x)-1), (sqrt(3+x)-sqrt(x))/x

Limit x tends to 1 x square - root x / root x - 1 l NEB

`underset(x to 1-)lim (sqrtpi-sqrt(2 sin^(-1) x))/sqrt(1-x)` is equal to

Prove that:`lim_(x to 0)(sqrt(1+x)-1)/(log(1+x))=(1)/(2)`