Ant & Honey Puzzle || A Challenge for your Genius Mind

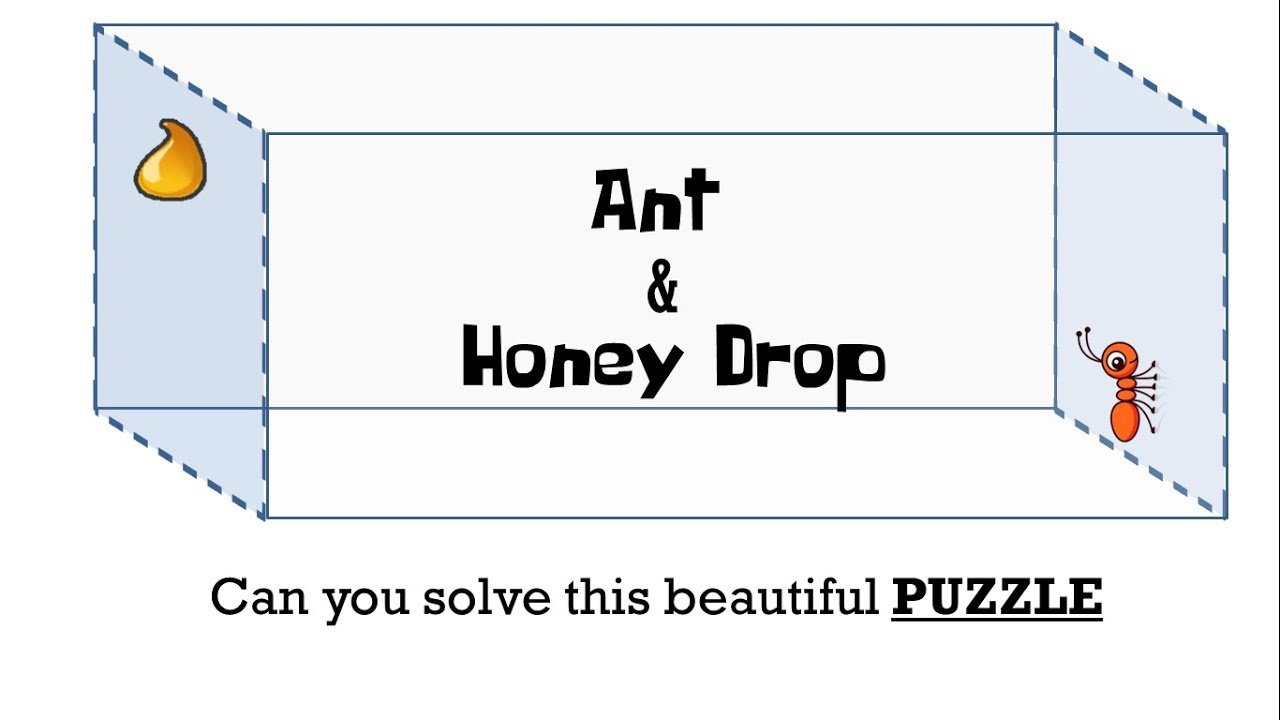
Inside a rectangular box, with length 30 inches and height and width 12 inches, an ant is located at the middle of one side
1 inch from the bottom of the box.

There is a drop of honey located at the middle of the opposite side, 1 inch from the top.
Please note that the ant and the honey drop are at the middle of the sides, that means 6 inches from the edges.
Puzzle:
What is the shortest distance the ant would need to crawl to get the honey?

The video has the best explanation for the Puzzle solution.

Your ""Likes"" and ""Shares"" really encourage me to make more and more videos.

Also try the following puzzles:
Can you solve the Tricky Puzzle || The Clever Commuter || Logical Puzzle

Difficult Puzzle || 25 Horses Race || Asked in Google and Microsoft Interviews

Seemingly IMPOSSIBLE Fox Puzzle || Fox in a Hole || Asked in Google Interview

Parking Lot Puzzle || Can you solve this Math problem

Cheryl's Birthday Puzzle || Viral Puzzle on Facebook and Whatsapp

Dark Room and Coins Puzzle || Can You Solve this Logic Puzzle

You can follow my facebook page of Logically Yours( Mohammed Ammar ):

Please comment below your answers and suggestions. Also LIKE the video and SUBSCRIBE to my channel if you are new.

[dipaksen]

Both ant & honey are inside the box. How could I think outside the box????!?!?!?!

[loganwolfpack]

Stand the box up right, the ant drops straight down and only crawls 10 inches to the honey

[mdfirdosh]

My physics professor asked this question in 2016. That time i took one day to give him correct answer.Now i feel blessed

[satyamsingh]

When your cable wire is short.. use this calculation...

[MurtuzaBookwala]

Trial and error is fine, but how do you prove your solution is optimal? What if there is a better way to unfold with a shorter path?

[PlokgiH]

type of ant wasn't specified, 0 inches of crawling required, ant flies

[ellaenchanted]

My assumption was originally 31" assuming the droplet would drop; however, that assumes that the drop could fall faster than the ant could crawl. Even if the honey drops, it could just as easily still be halfway up by the time the ant reaches it. I would love to see this problem with added data asking for the time at which the ant reaches the drop i.e. if the ant can travel this quickly and the drop moves down at this rate, how long would it take the ant to reach the drop if the most effective route is taken/where will the drop be etc.

[EddieOtool]

Fun fact:
The ant on its trajectory, from P0 to P1 (given a point at every corner), finds itself effectively further away from the honey drop by nearly 3/8th of an inch (31.6227... at P0, 31.9618... at P1 according to my 3D CAD re-enactment).

Conclusion #1: Sometimes, in order to attain your goal as quickly as possible, you have to seemingly move away from your objective for a short while (that's usually when you get others to complain about your incomprehensible behavior).

Conclusion #2: Since I doubt an ant has the ability to suffer feeling itself drifting further away from its objective even for the smallest moment, I doubt the optimal solution be true-to-life.

Question #1: I wonder what the path on the box would look like if the premise was instead that every step it took had to bring it the closest possible to its goal (3D straight line), no matter the total length of the path thus created. It would probably go up 10 inches right away because it would be the fastest immediate gain, but after that it would have to choose among multiple paths that would take it away from its goal for a moment. Without mathing it, I suppose it would still elect the 42 inch simplest trajectory... after going circles for half an hour trying to get immediately closer to its goal, to no avail. In fact, on this trajectory, it doesn't have to go more than 0.0166..." further afar from its goal when it has to.

Question #2: I did wonder what the graph of the 3D distance to goal look like, but when I graphed it it was way less crazy than I expected (pretty much a straight line aside from the initial increase). Interestingly enough, whoever came up with the dimensions of this box did a good job in chosing easily computable figures: Apart from the sum of the squares which equals to an easy enough number to root without assistance, the 5 segments of the trajectory, albeit all diagonals, have lengths of 1.25, 8.75, 20, 8.75, and 1.25 inches respectively, for a sum of 40 inches. Pretty neat!

Bonus round:
If you've read all the way down here, here's one for you: A water lily double its size every 4th day. It starts up at 1 inch diameter, and after 60 days it completely covers the lake on which it is growing. Question: If the lake's diameter is one third that of an average lake on this county, after how many days will the lily cover half the lake's area?

[leepuihin]

The number of comments saying the ant can't unfold the box really kills me. It's a method for you to find a straight line (I.e. Shortest path) and the ant doesn't have to unfold the box to walk that path. The final illustrations clearly shows that the ant is crawling inside the box while it's folded. Both of these are very obvious and clearly explained in the video.

[aeromodeller]

There is a very simple search method that makes it clear that 40" is the minimal path on the surface of the box. Roll the box along a flat plane and trace each rectangle onto the surface. As you trace each rectangular side, also fold the end panels out and down onto the surface and trace them, marking the start and endpoints. Roll until you have traced five sets of panels. You can see that as the end panel rolls along the edges of the center rectangles, the start point will have four possible positions, on each of the four sides of the end squares. Now by inspection you can connect each starting point with any of several nearby endpoints on the other side of the diagram. You can quickly establish a shortest path for each start point position and you find that the shortest of those shorter paths occurs when the start point and the end point are both 1" from the end of their respective center rectangle and the distance is 40". All other paths will be longer than that.

This is not thinking outside the box, this is thinking on the box.

[camerongray]

I admit, I did not think of unfolding the box, great video!

[Nellyontheland]

Zero if the box is tilted at an angle and it drops on his little ant head! I win.

[j.b.]

The first step in thinking outside the box is realizing that you are in one .

[tanmaypalkar]

I stick to my theory:-
1. ANTS DON'T CRAWL
2. HONEY WILL EVENTUALLY DROP DOWN WITH TIME

[soumayadeepganguly]

Thank you very much.
Many a time I saw the lizard running for it's prey in a zig-zag way in the walls.


I thought that, they doesn't have the brain.

But today I realized that, they have the ability to sense the shotest path.


Thank you very much for helping to choose my next topic for my research

[donaldbaker]

Why is everyone forgetting that the shortest distance between two points is that point. If you bend space the ant doesn't have to travel at all, it simply arrives at the honey.

[bobofett]

39 3/4 inches. The ant's a quarter inch long. Even less if it has long lips.

[LBF_NotGnome]

Collapse the honey side down to the floor. This makes it 11in closer to ant. Then do same with ant side making it 1in closer to honey.

We're left with floor 30in - 11in -1in = 18in

[avnishkumar]

Ant reached and ate the honey till the time you solved this

[shubhamborkar]

We can achive directly by making the cuboid smaller with dimension 10*12*30...
N can find direct shortest distance as sum of two sides of cuboid as 10+30=40....