[UT#66] Longueur d'une courbe (Introduction)

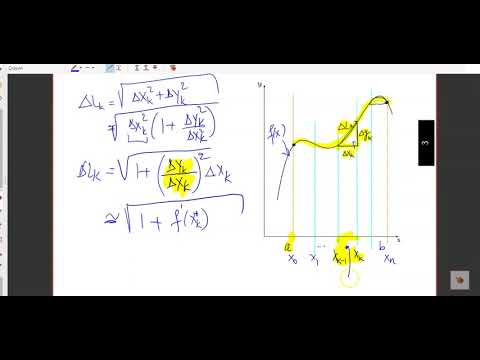
Dans cette émission, j'explique comment obtenir raisonnablement une formule qui permette de calculer la longueur d'une courbe. Si l'intégrale est bel et bien un moyen de calculer l'aire sous une courbe, c'est aussi une intégrale qui va nous permettre de triompher, mais comment ?

🕒 Repères temporels:
0:00 - Introduction
1:09 - Idées fondamentales
3:07 - Première approche (Tangentes)
7:53 - Deuxième approche (Interpolation)
9:44 - Ouverture

🎥 Émissions connexes:

✒️ Notions abordées: longueur d'une courbe, théorème de Pythagore, tangente à une courbe en un point, interpolation lagrangienne, somme de Riemann, forme indéterminée.
🌞 Bonne écoute !

🔸Tu apprécies le contenu que je produis ?
🔸Tu souhaites que je réalise davantage de vidéos ?
🔸Tu souhaites me remercier pour ce que cette chaîne t'a apporté ?

[gerardpeyrouty]

Super clair ! Ça m'aurait vraiment aidé il y a 50 ans !!
Merci.

[jnx]

Vraiment encore une fois très bien expliqué ! Bravo. La difficulté que l'on peut rencontrer pour calculer la longueur de certaines courbes, c'est d'arriver à trouver la primitive correspondante... Pas toujours simple.. 😉.

[ossejeancalvin]

Formidable, pédagogique, enrichissant. vous avez l bonne approche pour exposer les nouvelles notions aux passionnés de mathématiques, notamment la notion d'intégrale. vivement de nouvelles videos a cet effet.

[smartcircles]

Merci pour vos émissions qualitatives, vos abonnés désirent aussi voir de l'algèbre, encore Bravo pour votre travail d'analyse somptueux 🙂

[etis]

Trop cool la vidéo !
J'aime beaucoup la coloration des variables, je suis convaincu qu'une bonne coloration lexicale et syntaxique des expressions peut énormément aider à la compréhension en soulageant le cerveau de la tâche fastidieuse de l'analyse de celles-ci (au même titre que l'on colore le code en programmation)

[gaetanf]

Pour les curieux, à noter que pour trier les fonctions ayant une longueur infinie même sur un intervalle compact, on peut calculer la V2-variation. Cela consiste à mettre au carré les accroissements infinitésimaux. C'est très utile par exemple pour s'intéresser aux variations du mouvement Brownien.

[jonahfracchia]

J'ai refait l'integralité de la chaine et je troive que dans l'ensemble, les vidéos de cette chaîne sont excellentes car expliqué de façon précise et méthodologique de façon à ce que l'on comprenne les enjeux. Cependant il manque clairement des petits exercices à la fin qui permettent de mettre en application ce qui a été vu de façon concrète. N'oublions pas que un prof nous demande en devoir de résoudre des exos et non pas d'expliquer un cours.
Ce qui pourrait aussi être intéressant, c'est quand un thème a été exploré, il faudrait une vidéo avec un exercice un peu plus grand qui mettent en application les notions abordées et la méthode adéquat.

[franckdidier]

Et dire qu'on m'avait balancé la formule sans aucune explication, alors qu'une bonne monstration est en soi suffisante intellectuellement et intuitivement, alors merci pour ton approche vraiment pédagogique et aussi ludique !

[jamesmaxwell_it]

Excellent 😊👍....je ne m'étais jamais poser la question, j'ai la réponse, Riemann est vraiment partout ..

[mathspe]

C'est quand même magnifique comme méthode. Merci

[jcfos]

Très intéressant. Un très bon niveau universitaire. J'abuse encore une fois : à quand des vidéos sur les tenseurs, leurs applications, leurs utilisations, leurs fonctionnalités intrinsèques ? Sinon, toujours au top

[guillaume]

Hello!
J'ai 28 ans et me souviens de cette question que j'avais eu à l'oral de Maths de Centrale ! Heureusement que j'avais la formule en tête mais en revoyant la démonstration, tout semble logique :)

[percy-yuikoze]

Super vidéo !
Pour la démonstration avec l'interpolation j'ai fait la chose suivante:
Si f est de classe C1 sur l'intervalle [0, 1], alors pour tout a élément de [0, 1], la limite [f(x) - f(a)]/[x-a] quand x->a existe et vaut f'(a) (1).
La dérivée est de classe C0 donc elle est continue.
1+f'(x)² > 0 pour tout x élément de [0, 1] et la fonction 1+f'(x)² est continue sur [0, 1], donc sqrt(1+f'(x)²) est aussi continue sur [0, 1] (2).
On peut réécrire l'expression n²[f((k+1)/n) - f(k/n)]² comme une fraction avec [f((k+1)/n) - f(k/n)]² au numérateur et [(k+1)/n - k/n]² (soit 1/n²) au dénominateur.
Quand n tend vers l'infini, (k+1)/n tend vers k/n.
On reconnaît un taux d'accroissement, et quand n tend vers l'infini, ce dernier tend vers f'(k/n) par (1).
Toutefois, je bloque un peu car [f((k+1)/n) - f(k/n)]² / [(k+1)/n - k/n]² vaut f'(k/n) que quand n tend vers l'infini. Donc on ne peut pas (?) reconnaître une somme de riemann en posant g(a + b * k(b-a)/n) = sqrt(1+f'(k/n)²) avec a = 0 et b = 1, ce qui nous mènerait au résultat souhaité car g est continue par (2).

[ahcenecanpos]

Formidable explication ; super analyse du problème poser sincèrement . Pour la première fois, j'ai l'impression que les mathématiques ont une saveur qu'on peut des videos sur résolution d'équation diophantienne a 3 inconnus degré 2 exemple: z=ax²+bxy+cx+y avec a, b, c des nbres naturels et x, y, z les inconnus aussi entiers naturels .

[baptiste]

Sa fait partie de ce genre de résultats que j'ai moi même dérivée ! Bien sur je savais quand même déjà vaguement où allez et ce à quoi le résultat ressemblait car je l'avais croisé deux trois fois. Mon approche était légèrement différente de ce que vous faite dans la vidéo cependant, en voici un résumé.
Je suppose que je connais déjà une fonction L qui me donne la longueur de la courbe f sur l'intervalle [0:t], puis je m'intéresse au cas t+h avec l'idée de rendre h très petit et d'approximer l'a courbe avec une ligne droite, et pareil avec un peu de Pythagore on s'en sort très bien comme ça aussi, l'avantage c'est que cette démonstration ressemble beaucoup à la démonstration que l'aire sous la courbe d'une fonction sur un intervalle [a;b ] est l'intégrale de cette fonction sur cet intervalle, après je pense pas que ce soit aussi rigoureux que ce que vous proposer dans cette vidéo.

[Bertrandrobintaudou]

bravo
vraiment sympa ta vidéo ...
c'était une question que je posais ...
j ai une explication maintenant

[sub_a_roues]

Bonjour. Tombé par hasard suite aux suggestions ... Très intéressant !
Mais j'ai pas le niveau 😅
Mais pour le reste, vu que je travaille souvent sur des plans papier, un curvimètre et c'est plié 👍🏻

[sebastienc]

Hasard de l'algo de google, je tombe ici. Merci pour ça :)

[pzorba]

Très bel exercice pour être prêt le jour de la rentrée. Un peu limite pour des élèves de terminale...

[gaspard]

Pour la solution à la fin, j'ai vu personne faire ça alors que de cette manière ça se montre très rapidement :
Par le th d'égalité des accroissements finis, quelque soit k il existe C(k) dans [k/n, k+1/n] tel que f(k+1/n) -f(k/n) =1/n * f'(C(k)).
Donc le somme de départ est égal à : 1/n*sum(1+f'(C(k)))
Avec C(k) dans [k/n, k+1/n] donc f' étant continue car f est C1 on utilise la somme de Riemann.