filmov
tv
Limit with a Cube Root - Factoring is the Way to Go! | Limits | Calculus | Glass of Numbers

Показать описание
In this video, we look at a limit with a cube root.
No, don't multiply the numerator and denominator by the conjugate of the expression.
It doesn't work. Instead, we factor x - 64. How do we do it? Watch this video for the details!
📺 Subscribe to my channel for Math Learning!
Please help me by subscribing to my YouTube channel. I want to use my free time to make a lot of math videos to help others and to make education available to the world. Your Likes and Subscribing will help this channel be reached by more people. Thank you!
Follow me:
Ayúdame suscribiéndome a mi canal de YouTube. Quiero usar mi tiempo libre para hacer muchos videos de matemáticas para ayudar a otros y hacer que la educación esté disponible para el mundo. Tus Me gusta y Suscripciones ayudarán a que más personas lleguen a este canal. ¡Gracias!
請訂閱我的YouTube Channel, 我會製作更多與數學相關的視頻,讓世界各地的朋友用簡單的方法學習數學(數學考試一定A)!請用您的訂閱和點贊支持我,並在留言區與我討論!謝謝!
#Calculus #Limits #YouCanLearnAnything
No, don't multiply the numerator and denominator by the conjugate of the expression.
It doesn't work. Instead, we factor x - 64. How do we do it? Watch this video for the details!
📺 Subscribe to my channel for Math Learning!
Please help me by subscribing to my YouTube channel. I want to use my free time to make a lot of math videos to help others and to make education available to the world. Your Likes and Subscribing will help this channel be reached by more people. Thank you!
Follow me:
Ayúdame suscribiéndome a mi canal de YouTube. Quiero usar mi tiempo libre para hacer muchos videos de matemáticas para ayudar a otros y hacer que la educación esté disponible para el mundo. Tus Me gusta y Suscripciones ayudarán a que más personas lleguen a este canal. ¡Gracias!
請訂閱我的YouTube Channel, 我會製作更多與數學相關的視頻,讓世界各地的朋友用簡單的方法學習數學(數學考試一定A)!請用您的訂閱和點贊支持我,並在留言區與我討論!謝謝!
#Calculus #Limits #YouCanLearnAnything
Limit with a Cube Root - Factoring is the Way to Go! | Limits | Calculus | Glass of Numbers
Evaluate the limit of (cube root of (x+8)-4)/(square root of (x-40)-4)
Limits by Variable Substitution for Cube Root Function
A Limit With A Cube Root
Limits with Cube Roots | Evaluating limits invovling Cube Roots without l'Hopitals | Calculus
Explore Limits by Method of Variable Substitution For Cube Root Functions
Limit with Cube Root with Variable Substitution
Limits with Function of square root and cube roots
Class 12 - 022 - Definite Integration
The Cube Root Conjugate in Limits
How to Substiture Cube Root to Find Limit of Indeterminants
limit rationalize cube root
One Side Limits of Transformed Cube Root Function
LIMIT WITH CUBE ROOT - CALCULUS EXERCISE
Limit involving a cube root
How to Rationalize Cubic Roots Concept with Solution
RATIONAL and CUBE ROOT LIMIT FUNCTIONS TENDING TO INFINITY WITH ASSIGNMENT (PRECALCULUS)
How to Find the Limit of the Cube Root of x as x Approaches Infinity #shorts
Calculus limits with cube roots
Limit by Variable Substitution Method for Cube Root finction
Limits Level 2 Examples with difference of cubes IIT JEE AP Calculus
Finding Derivative of a Cube Root Function Using Limit Definition
Evaluating Limits By Factoring
Limits at Infinity - Example 7
Комментарии
 0:09:17
0:09:17
 0:06:05
0:06:05
 0:04:05
0:04:05
 0:07:12
0:07:12
 0:20:40
0:20:40
 0:04:37
0:04:37
 0:05:03
0:05:03
 0:05:47
0:05:47
 0:47:46
0:47:46
 0:11:02
0:11:02
 0:05:50
0:05:50
 0:02:46
0:02:46
 0:04:35
0:04:35
 0:02:55
0:02:55
 0:09:51
0:09:51
 0:05:41
0:05:41
 0:02:32
0:02:32
 0:00:25
0:00:25
 0:26:02
0:26:02
 0:06:11
0:06:11
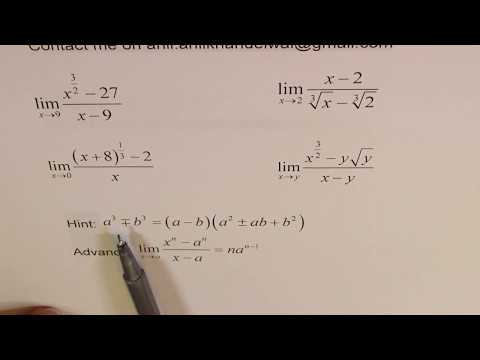 0:22:36
0:22:36
 0:05:10
0:05:10
 0:11:35
0:11:35
 0:04:42
0:04:42