Deriving Input Demand Functions from Cobb-Douglas Production Function

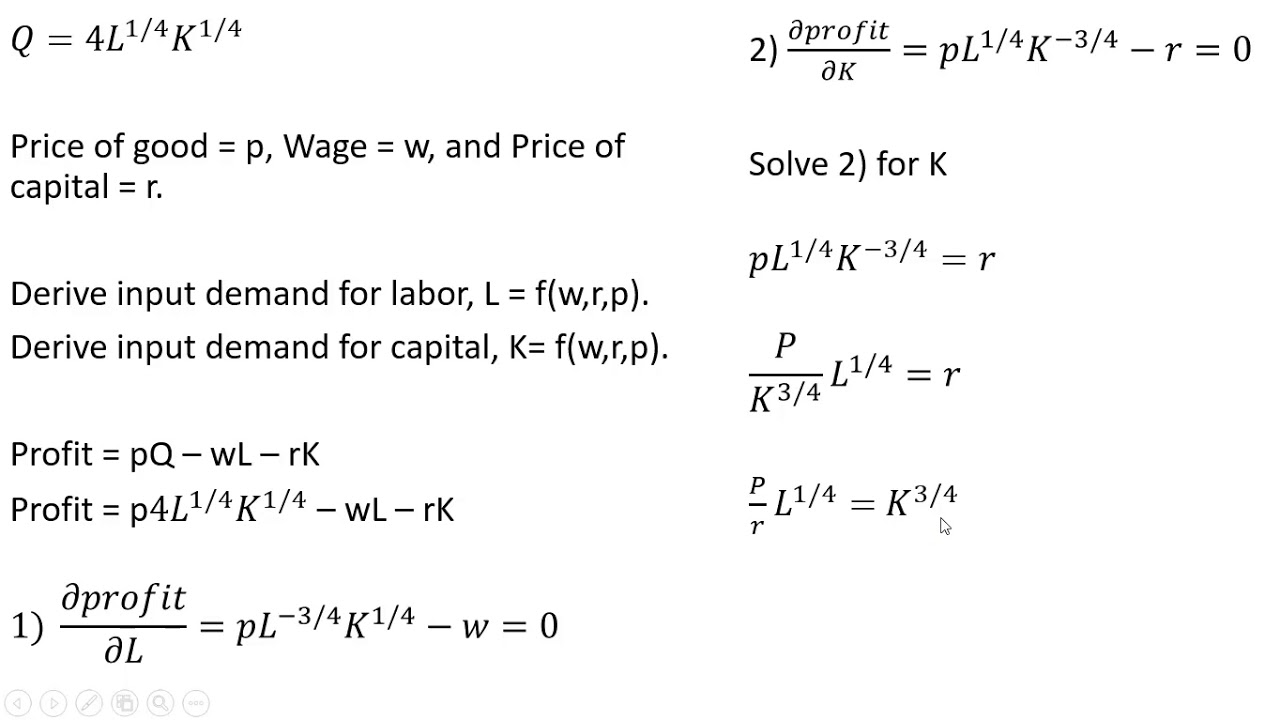
preview_player
Показать описание
This video derives labor demand = f(w, r, p) and capital demand = f(w, r, p).

  1. Economics in Many Lessons
  2. labor and capital input demands
  3. how to find labor input demand
  4. how to solve capital input demand
Рекомендации по теме
Deriving Input Demand 0:06:39

Deriving Input Demand Functions from Cobb-Douglas Production Function

Deriving Input Demand 0:04:23

Deriving Input Demand Functions

Mathematical Derivation of 0:08:37

Mathematical Derivation of Input Demand

Derivation of Input 0:25:59

Derivation of Input Demand Function @ecologue8202

Derive a Production 0:03:16

Derive a Production Function from Cost function

Production function: Derive 0:02:27

Production function: Derive profit function and factor demand function

Deriving a Production 0:04:13

Deriving a Production Function from Cost Function Using Sheppard's Lemma

Derived Demand 0:02:22

Derived Demand

Cobb-Douglas: Conditional input 0:11:38

Cobb-Douglas: Conditional input demands, Long-run Total Cost, Shephard's Lemma

Conditional Demand for 0:11:38

Conditional Demand for inputs

Derive Labor Demand 0:01:22

Derive Labor Demand Function From q = 20ln(L + 1)

Derivation of Factor 0:05:50

Derivation of Factor Demand Function from Profit Function | Hotelling's Lemma

Profit Maximization: Input 0:07:07

Profit Maximization: Input Demand Function (Derivation) | Microeconomic Analysis | ECO614_Topic168

Input Demand Function, 0:14:54

Input Demand Function, Output Supply Function and Profit Function Faizan Noor Bhutta #Microeconomics

DERIVING DEMAND AND 0:10:24

DERIVING DEMAND AND SUPPLY FUNCTIONS

Perfect Complement Utility 0:04:36

Perfect Complement Utility Funtions: Deriving Demand Functions

Firms: Switching between 0:04:16

Firms: Switching between conditional and unconditional factor demands

How to Derive 0:04:26

How to Derive Consumer Demand Functions from Cobb-Douglas Utility Function

deriving profit function 0:04:30

deriving profit function from a production function

Microeconomics - Deriving 0:12:10

Microeconomics - Deriving a Firm's Short Run Demand for Labor (Marginal Revenue Product)

#6 Derivation of 0:13:10

#6 Derivation of Demand Function : CES utility function

Mathematical Derivation of 0:06:09

Mathematical Derivation of Expansion Paths and LRTC Functions

Input Demand function#1, 0:23:55

Input Demand function#1, Lect-70

Conditional Factor Demand 0:17:01

Conditional Factor Demand Function and Comparative Statics of Cost Minimization

Комментарии
Автор

Hi. Thank you so very much for this wonderful precise explanation. It was extremely helpful. God bless you
A hug from Mozambique 🇲🇿

adrianamacamo
Автор

Thank your for your video! From this step, pluging the optimal inputs K and L in the production function you can also find the output supply function. In order to find the conditional demand functions for K and L, should you set up the Lagrange C s.t. Q- F(q, l) and find the solutions or is there a faster way?

chrislemminatorgr
Автор

Tough algebra, but quite helpful video Thank you!

munshikhan
Автор

Can't we divide the partial derivative with respect to l and partial derivative with respect to k and set it equal to w/r and solve for l or k. (i.e, mpl/mpk = w/r)
PLEASE REPLY!

Amit-cngg
Автор

can you make video for single variable input; labour

DanielSeniyu
Автор

Wait, where did the 4 in the equation disappear when you derive in the beginning!?

skrapsaker
Автор

Hello. I watched your lectures and found these lectures are very helpful. Now i need your help to solve this equation.
If our total cost is TC= Q3 (Q cube) --8Q2 (minus 8Q square) +57Q + 2 and demand function is p = 45 - (minus) 0.5Q.

Then how to find the level of output and price at which the price is maximized?
And
How to find the level of output and price at which total revenues are maximized?

arifhussain