Calculating Simple Interest | Financial Mathematics

How do we calculate simple interest? How do savings grow when they earn simple interest? That's what we'll go over in today's financial math lesson!

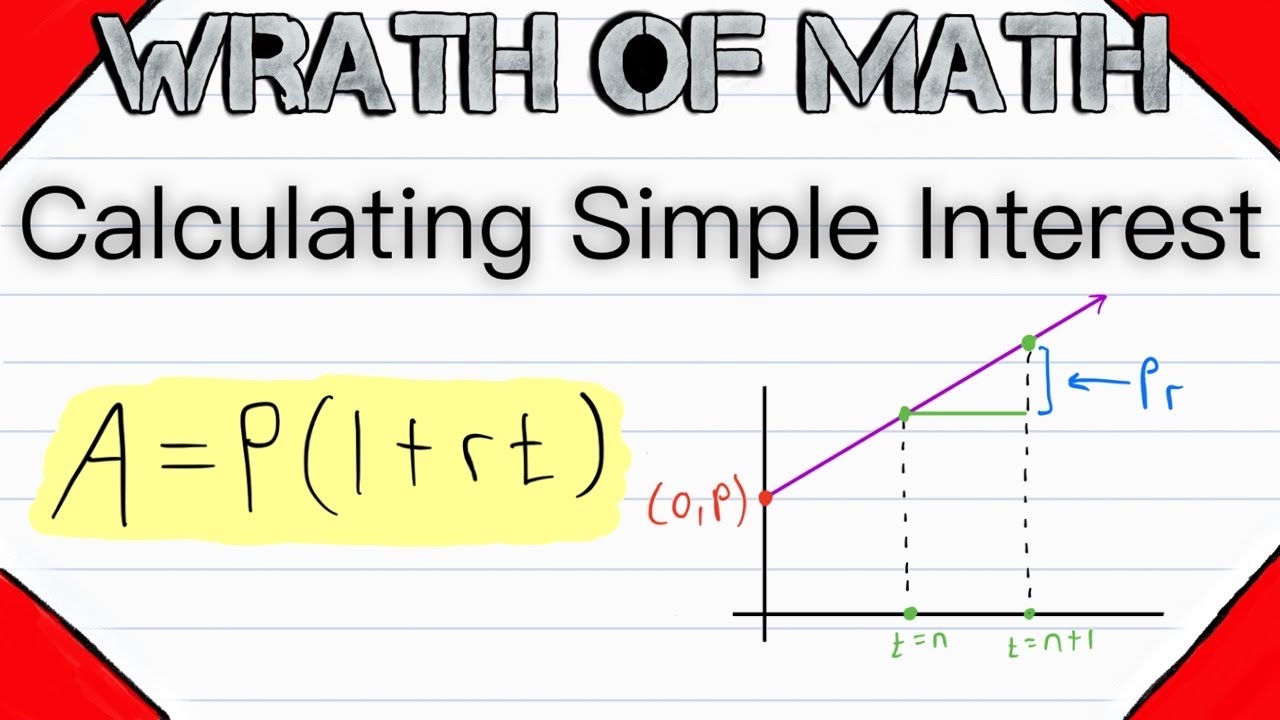
If a principal amount P is invested in a fund that earns simple interest at a rate r, then P*r is earned in interest every interest period. If r is an annual simple interest rate, then P*r is earned every year. If r is a monthly rate, then P*r is earned every month, and so on. Thus Prt is the total amount earned in interest at time t. Note that t needs to measured in the same units of time as the simple interest rate.

Since the principal amount P remains in the fund at all times, the total amount in the fund at time t is P(1 + rt). This distributes to P (the principal amount) plus Prt (the amount earned in interest). A fund earning simple interest grows as a linear function of time. The primary difference between simple and compound interest is that simple interest is earned only on the principal investment whereas compound interest is earned on the principal amount as well as the already earned interest. Watch the full video for more details!

SOLUTION TO PRACTICE PROBLEM:

We are given that 10 is invested in an account earning simple annual interest at a rate of 2%. How much is in the account after 3 years and 3 months?

We can use the formula A = P(1+rt). The amount in the account after 3 years and 3 months is 10*(1+2%*3.25). Note in this expression, t = 3.25 because 3 years and 3 months is 3 and a quarter years - we want t to be measured in years because our simple interest rate is annual. So the amount is 10*(1+2%*3.25) = 10.65. Thus, 10.65 - 10 = 0.65 has been earned in interest.

I hope you find this video helpful, and be sure to ask any questions down in the comments!

+WRATH OF MATH+


Follow Wrath of Math on...

[clairupshon]

Omg.. thank you so much Sean. My teacher today was very impressed by me because I could answer a simple interest question even though we have not come across it yet. I thanked him for the appreciation but also said that the credit goes to Sean from Wrath of Math. My teach told me that he loved your math videos and told me to give his regards.