filmov
tv
Calculus 1, Session 30 -- Riemann sums
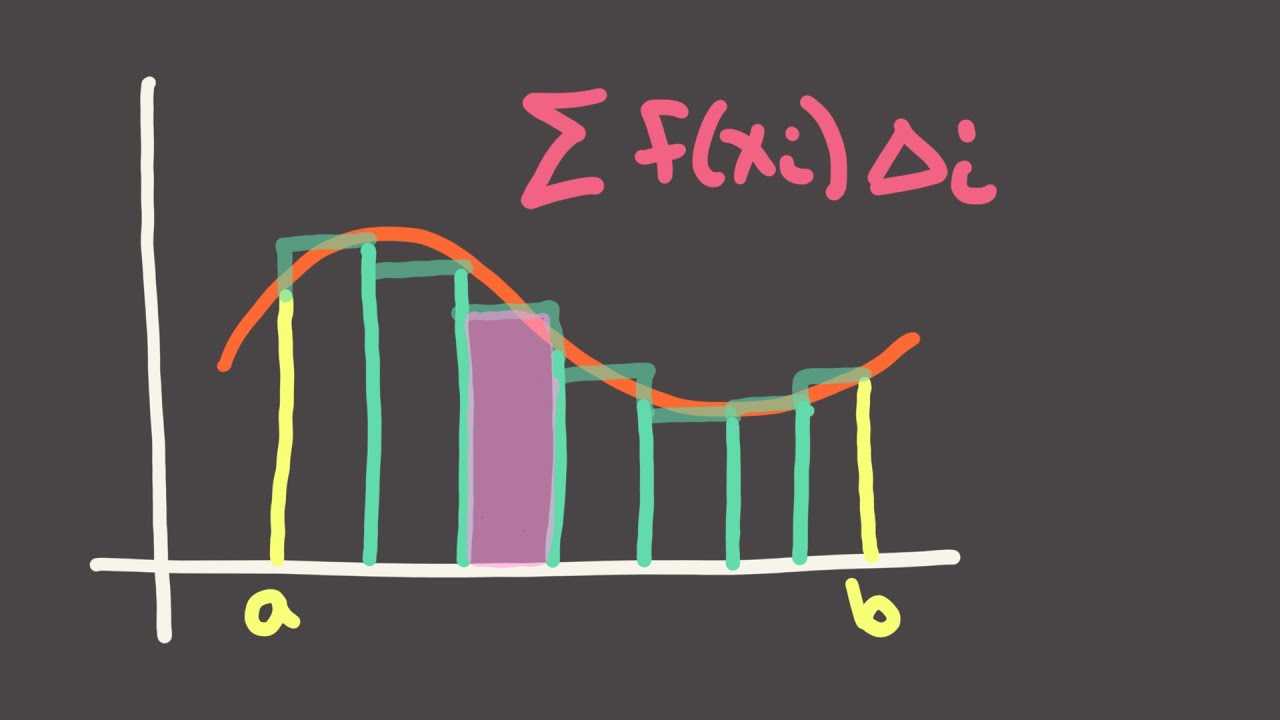
Показать описание
Calculus 1, Session 30 -- Riemann sums
A Year's Worth of Calculus in 1 Minute
How To Get a 5 on AP CALCULUS in 60 Seconds!
Calculus 1 Final Exam Review
Calculus 1 | 1.3 (Composition of functions) | Part(2)
Calculus 1 | Sec 2.2 (The Limit of a Function) | Exercises
Calculus 1, Session 31 -- Definite integrals; areas by limits of Riemann sums
ALL OF Calculus 2 in 5 minutes
Calculus NCEA Level 2 in 15 hours | Part 3
MATH BUDDY Topic: Limit (Final Acceleration for Calculus 1 - Session 3)
Calculus 1, Session 15 -- More practice with the chain rule
ALL of calculus 3 in 8 minutes.
Calculus 1, Session 26 -- Optimization
Zoom session Last Minute AP Calculus Exam Review (May 11, 2020)
Calculus 1, Session 36 -- Separable differential equations
4/30/20 Calculus Zoom Session
Calculus 1, Lec 30: More Proofs, Cool Parametric Equation Examples (Find the Speed & Distance (F...
Calculus 1, Session 35 -- Substitution with definite integrals
Calculus 30 1.2 #1, 2, 4 homework limits of functions 2021
AP Calculus 30L- Definite Integrals are the key to counting BIRDS! And for scaring them!!
Calculus 1, Session 11 -- Derivative as motion
Calculus 1, Session 27 -- More optimization practice
Calculus 3, Session 30 -- Jacobian; multivariable substitution
Vector Calculus - SESSION NO 30 SIDDHARTH SABHARWAL AIR 1|
Комментарии
 0:48:39
0:48:39
 0:01:09
0:01:09
 0:01:03
0:01:03
 0:55:58
0:55:58
 0:20:45
0:20:45
 0:39:03
0:39:03
 0:48:14
0:48:14
 0:06:09
0:06:09
 1:08:10
1:08:10
 0:57:37
0:57:37
 0:45:35
0:45:35
 0:08:10
0:08:10
 1:03:10
1:03:10
 1:39:28
1:39:28
 1:00:51
1:00:51
 0:08:37
0:08:37
 1:01:18
1:01:18
 0:46:51
0:46:51
 0:11:04
0:11:04
 0:00:49
0:00:49
 1:09:07
1:09:07
 1:06:45
1:06:45
 1:12:02
1:12:02
 1:37:15
1:37:15