filmov
tv
Gauss-Jordan Elimination Example

Показать описание
Using Gauss-Jordan Elimination to solve a system of linear equations requires you to use elementary row operations to convert an augmented matrix that represents your system of equations into the appropriate final form. The example focused on here has only one solution to the system of equations.
#gaussjordanmethod
#linearequations
#solvesystemofequations
#linearalgebra
#JoeCMath
0:00 Introduction
0:20 Introduce example matrix
1:06 Making row 1, column 1 equal 1
2:05 Making row 2, column 1 equal 0
3:15 Making row 3, column 1 equal 0
4:29 Making row 2, column 2 equal 1
4:57 Making row 3, column 2 equal 0
5:29 Making row 3, column 3 equal 1
6:03 Making row 2, column 3 equal 0
6:37 Making row 1, column 3 equal 0
7:15 Making row 1, column 2 equal 0
7:37 Getting the solution from the final matrix
#gaussjordanmethod
#linearequations
#solvesystemofequations
#linearalgebra
#JoeCMath
0:00 Introduction
0:20 Introduce example matrix
1:06 Making row 1, column 1 equal 1
2:05 Making row 2, column 1 equal 0
3:15 Making row 3, column 1 equal 0
4:29 Making row 2, column 2 equal 1
4:57 Making row 3, column 2 equal 0
5:29 Making row 3, column 3 equal 1
6:03 Making row 2, column 3 equal 0
6:37 Making row 1, column 3 equal 0
7:15 Making row 1, column 2 equal 0
7:37 Getting the solution from the final matrix
Gauss Jordan Elimination & Reduced Row Echelon Form
❖ Using Gauss-Jordan to Solve a System of Three Linear Equations - Example 1 ❖
Algebra - Solving Linear Equations by using the Gauss-Jordan Elimination Method 2/2
Gauss-Jordan Elimination
❖ Using Gauss-Jordan to Solve a System of Three Linear Equations - Example 2 ❖
Manipulating Matrices: Elementary Row Operations and Gauss-Jordan Elimination
Gaussian Elimination and Gauss Jordan Elimination (Gauss Elimination Method)
Guide to Gauss-Jordan Elimination (and Solving Systems of Equations) | Linear Algebra
Gaussian Elimination & Row Echelon Form
Gaussian Elimination and Gauss-Jordan Elimination Four-Variable Linear System
❖ Inverse Matrix Using Gauss-Jordan / Row Reduction , Example 1 ❖
Algebra 55 - Gauss-Jordan Elimination
🔷11 - Gauss Jordan Elimination and Reduced Row Echelon Form
Gauss Jordan Elimination Example
Gaussian Elimination With 4 Variables Using Elementary Row Operations With Matrices
Gauss-Jordan Elimination Method - Sample Problem
Gauss-Jordan elimination method with calculator.
Solving System of Linear Equations: Gauss-Jordan Reduction
Gaussian elimination | Lecture 10 | Matrix Algebra for Engineers
Gauss Jordan Method | System of Equation | Engineering maths | Mathspedia |
Gauss Jordan elimination method || Gauss Jordan elimination method in hindi
VTU Engineering Maths 1 Gauss Jordan Method interesting example(PART-2)
The Gaussian Elimination method - Matrices
Solving a System (2 X 2) Using Gauss-Jordan Elimination
Комментарии
 0:10:51
0:10:51
 0:07:12
0:07:12
 0:07:10
0:07:10
 0:12:49
0:12:49
 0:05:37
0:05:37
 0:10:36
0:10:36
 0:15:14
0:15:14
 0:11:44
0:11:44
 0:18:40
0:18:40
 0:17:29
0:17:29
 0:05:09
0:05:09
 0:15:36
0:15:36
 0:15:38
0:15:38
 0:38:15
0:38:15
 0:18:04
0:18:04
 0:15:08
0:15:08
 0:23:31
0:23:31
 0:12:19
0:12:19
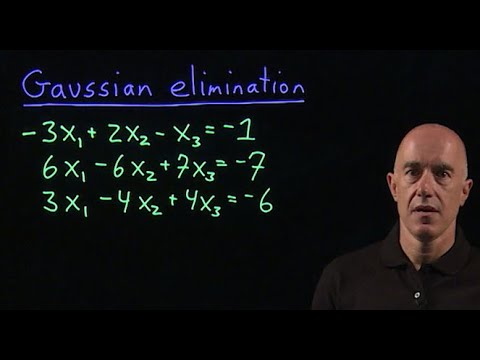 0:14:00
0:14:00
 0:16:03
0:16:03
 0:11:27
0:11:27
 0:06:44
0:06:44
 0:15:51
0:15:51
 0:04:32
0:04:32