По силам каждому ★ Найдите стороны треугольника на рисунке

@arinablog наш семейный канал
Задача от Шарыгина И. Ф.
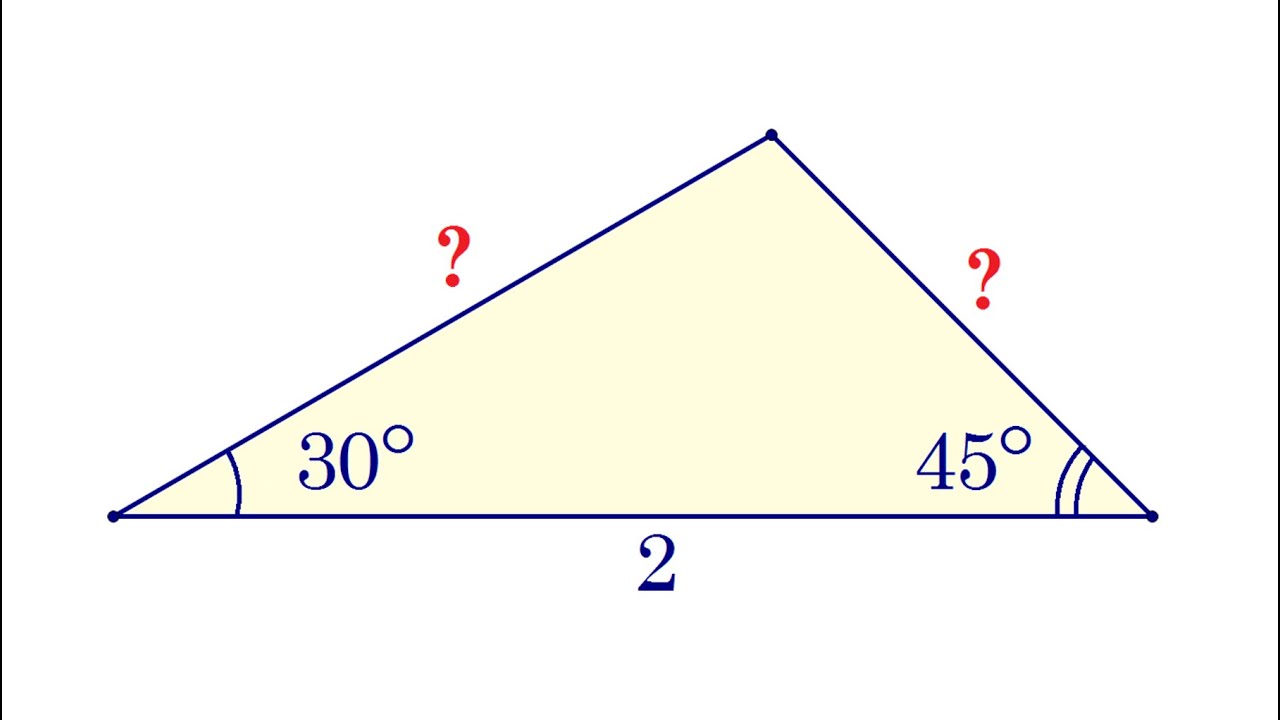
Сторона треугольника равна 2, а два прилежащих к ней угла равны 30° и 45°. Найдите две другие стороны треугольника.

[volodymyrgandzhuk]

Я сначала сделал то, что мне показалось проще всего, а именно - нашёл третий угол, он равен 180°-30°-45°=105°, а потом одну сторону нашёл по теореме синусов, а вторую по теореме косинуса.

[alvaro_sann-]

Можно было просто записать теорему синусов как x/sin30°=2/sin105°.
Да, синус 105 градусов не табличный но в чём проблема? Ведь Ну а дальше считаем всё, используем теорему косинусов для угла в 45 градусов. Ответ: sqrt(6)-sqrt(2) и 16-8sqrt(3).

[ИванСергеев-тч]

Можно воспользоваться формулой площади треугольника. Обозначив неизвестные стороны как х и у, записать площадь треугольника: S=1/2*2x*sin 30, S=1/2*2y*sin 45, S=1/2*xy*sin 105 и решить эти 3 уравнения как систему с 3-я неизвестными: двумя сторонами и площадью треугольника.

[iTrololo]

Можно было без квадратного уравнения: сторону с длиной (2-x) можно ещё вычислить как sqrt(3)*x из треугольника с углом 60 и гипотенузой 2x. Тогда sqrt(3) * x + x = 2 => x = 2 / (sqrt(3) + 1) = sqrt(3) - 1

[SurGainNoPain]

Можно и по теореме синусов:
2/sin(105°) = b/sin(30°) = c/sin(45°)
8/(√2+√6) = 2b
[8(√2-√6)]/-4] = 2b
-2(√2-√6) = 2b
b = √6-√2

-2(√2-√6) = c√2
c = [-2(√2-√6)]/√2 = -√2(√2-√6) = √2(√6-√2) = √12 - 2

b = √6-√2
c = √12 - 2

[ВладимирВалерьевич-хс]

Благодарю за очередную разминку для мозга.

[nazimavaleeva]

Тут увидела комментарии насчёт теоремы синусов, я думаю вы правильно выбрали этот метод он универсальный, возможно задача в разделе где ещё не проходили эту теорему

[nurlybekmoldagaliev]

Решается в уме.
Принимаем высоту равной Х, тогда сторона прилегающая к углу 30° равна 2*Х, а её проекция на основание (√3)*Х, проекция стороны прилегающей к углу 45° равна Х. Тогда длина основания (1+√3)*Х, следовательно Х=2/(1+√3). Избавляемся от иррациональности в знаменателе Х=2*(√3-1)/((1+√3)*(√3-1)), Х=(√3-1). Длина сторон 2*(√3-1), √2*(√3-1).

[АннаПономаренко-эл]

Эта задачка не столько сложна, сколько интересна — интересно, сколькимя способами можно её решить.
За несколько секунд в комментах обнаружила как минимум ещё три решения, кроме авторского (одно моё, через теорему синусов).

[ЛарисаРашевская-эщ]

Клево, я так же решила, спасибо, с вами интересно!

[ЗояШаромет]

Самое простое решение: х:(2-х)=tg30° .Просто выразить tg30° из левого треугольника.

[sashaonzhe]

Теорема синусов? Многие из вас вспомнят эту теорему через 20-30 лет после окончания школы? А вот теорему Пифагора, наверное, последний двоечник будет знать :)

[ИванПоташов-ою]

x можно было ещё найти из уравнения 2-х=x√3.

[anti_boss]

Вот такой


















































пробел в моих знаниях математики.

[AlexeyLapik]

Бе3 теорем чере3 определение тангенса. (2-x)*tg(30)=x*tg(45)
(2-x)/sqrt(3)=x
x=2/(sqrt(3)+1) или домножив до ра3ности квадратов x=sqrt(3)-1

[СтрекозаКомпьютер]

Отличное доказательство что учить синусы и косинусы не нужно)))

[mathmix]

Отличный способ решения для учащихся 8 класса!

[ТимурДаргелис]

Я тоже изначально положил высоту, однако дальше я пошёл через формулы площади треугольника: ah/2 и ab*sin(α)/2.

[MiceRus]

А почему не использовался тангенс? С ним же вообще все в одно действие делается

[fizmat-online]

Это стандартная задача - решение треугольника по стороне и двум прилежащим углам.