filmov
tv
Linear Algebra - Lecture 39: The Characteristic Polynomial and Multiplicity

Показать описание
We talk about the characteristic polynomial of a matrix, and what polynomials can tell us about eigenvalues. We also introduce the algebraic and geometric multiplicities of an eigenvalue, and we talk about why the eigenvalues of a triangular matrix are its diagonal entries.
Please leave a comment below if you have any questions, comments, or corrections.
Timestamps:
00:00 - Introduction and definition
03:08 - 3x3 example
09:47 - Algebraic and geometric multiplicities
15:20 - The Fundamental Theorem of Algebra (sum of algebraic multiplicities)
20:25 - Eigenvalues of triangular matrices
#linearalgebra #eigenvaluesandeigenvectors #matrices #math
Please leave a comment below if you have any questions, comments, or corrections.
Timestamps:
00:00 - Introduction and definition
03:08 - 3x3 example
09:47 - Algebraic and geometric multiplicities
15:20 - The Fundamental Theorem of Algebra (sum of algebraic multiplicities)
20:25 - Eigenvalues of triangular matrices
#linearalgebra #eigenvaluesandeigenvectors #matrices #math
Linear Algebra - Lecture 39 - Orthonormal Sets
Linear Algebra - Lecture 39: The Characteristic Polynomial and Multiplicity
Linear Algebra Lecture 39 | Rank Nullity Theorem for Linear Transformations
Advanced Linear Algebra - Lecture 39: Using the Pseudoinverse to Solve Linear Systems
Linear Algebra 39 | Gaussian Elimination
Lecture 39 | Applied Linear Algebra | Vector Properties | Prof AK Jagannatham
Gil Strang's Final 18.06 Linear Algebra Lecture
Linear Algebra - Lecture 39
#Class 12th Maths || matrix || |By Rahul valiya lec-7
Lecture 39 || Orthogonal Basis || Orthonormal Basis || Linear Algebra ||
Length contraction, time dilation and velocity addition | Wild Linear Algebra B 39 | NJ Wildberger
Linear Algebra 39 | Gaussian Elimination [dark version]
Quantum Machine Learning - 39 - Using Quantum Linear Algebra for Learning
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
UPSC Mathematics Optional (in Hindi) | Linear Algebra | Lecture 39
Linear Algebra: Ch 2 - Determinants (39 of 48) Determinant of Matrices with A lot of Zeros
Algebra 39 - Inconsistent, Dependent, & Independent Systems
Lecture 39: Linear Algebra (dimensions of subspaces)
Linear Algebra | Rank of a matrix | Row -echelon form | Lecture-39
Linear Algebra | Lecture Series | Lecture 1
Linear Algebra Lecture 2: Examples of vector spaces
Linear Algebra-Class-39
Lecture 39 | Properties of Eigen values with proofs (Part I) | Linear Algebra | Tamil
Linear Algebra Lecture #3
Комментарии
 0:09:27
0:09:27
 0:23:26
0:23:26
 0:05:56
0:05:56
 0:19:49
0:19:49
 0:13:17
0:13:17
 0:36:15
0:36:15
 1:05:09
1:05:09
 0:32:44
0:32:44
 0:50:25
0:50:25
 0:25:44
0:25:44
 1:00:40
1:00:40
 0:13:17
0:13:17
 0:06:31
0:06:31
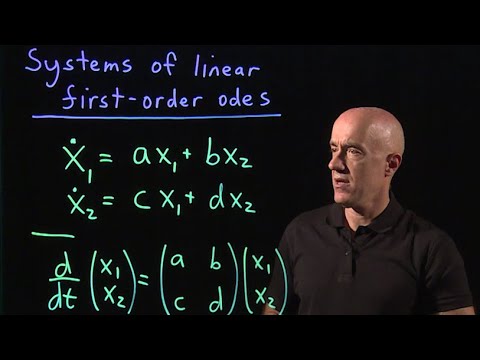 0:08:28
0:08:28
 0:51:38
0:51:38
 0:03:42
0:03:42
 0:07:26
0:07:26
 0:21:42
0:21:42
 0:21:41
0:21:41
 0:31:50
0:31:50
 0:36:39
0:36:39
 0:17:15
0:17:15
 0:22:34
0:22:34
 1:10:45
1:10:45