Zorn's Lemma, The Well-Ordering Theorem, and Undefinability (Version 2.0)

Zorn's Lemma and The Well-ordering Theorem are seemingly straightforward statements, but they give incredibly mind-bending results. Orderings, Hasse Diagrams, and the Ordinals / set theory will come up in this video as tools to get a better view of where the "proof" of Zorn's lemma comes from. Accepting the Axiom of Choice, which turns out to be equivalent to both Zorn's lemma and the Well-Ordering Theorem actually introduces a notion of an undefinable well-ordering; an order paradox -- specifically an impossibility of ordering the real numbers. The video can be broken up into the following sections:

00:00 Intro
00:48 Relations 101: Equality
02:52 Partial Order Definition and Examples
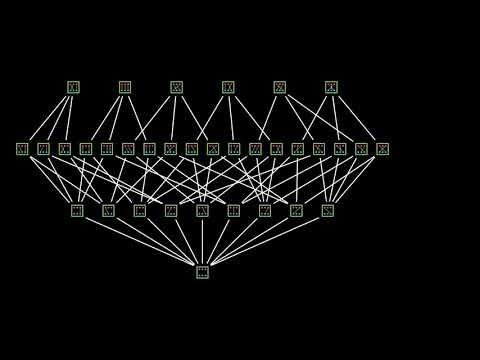
04:04 Hasse Diagram
05:12 Powersets and The Subset Partial Order
08:07 Zorn's Lemma
08:56 Ordinals in Brief
09:50 Sketch of Zorn's Lemma
12:18 Zorn's Lemma, The Well-Ordering Theorem, and The Axiom of Choice
13:06 The Well-Ordering Theorem and Undefinability

***Note in the section on Chains, two different chains are given even though I sound like I am talking about only one.

_____________________
_____________________

WHAT GEAR I USED FOR THIS VIDEO:

DISCLAIMER: Links included in this description may be affiliate links. If you purchase a product or service with the links that I include here, I may receive a small commission. There is no additional charge to you! Thank you for supporting my channel and for helping me create these free videos!

Subscriber Count as of release: 9,705 (+52 🙂)

#CHALK #ZornsLemma #SetTheory

[TheoriesofEverything]

I'm glad your channel exists. Great job on the general rigor in your videos.

[bemerald]

I found this video very helpful when learning about the topic in uni. Very well presented and explained, thanks :)

[AT-zrtv]

Thank you for this concise and highly informative video. I hadnt done math in 20 years, and this was one topic I particularly enjoyed. I really appreciated this refreshing trip to memory lane.

[sweehoelim]

Why do we need to use the fact that the ordinals are too big to be a set? When we keep adding upper bound elements to the chain, it seems you found a chain with no upper bound, which already contradicts the hypotheses of Zorn's lemma (every chain has an upper bound)?

[fzbartttt]

What about
2 3
/\
|
|
6
İt is a particular ordered set
And every chain (6, 2)(6, 3)have an upper bound
But no maximel for whole set

(the relationship is multiplay on (2, 3, 6)set)

[Necrozene]

First I learned about the Xorn monster in Dungeons and Dragons. Now I learn about the proper Zorn. Which is scarier?

[robfrost]

Assuming choice holds doesn't seem off at all. We don't need to know that AC is true. All we need to know is that assuming it true won't lead to any contradictions, and THAT, we know relatively safely, provided we pay attention to what we're doing.

[EmmanuelEytan]

This is good, but it's not an academic paper. Cut the first minute and a half. In a video like this, you need to start at the heart of the issue, not with an introduction. You can go back and provide an introduction as context later. But in video and film, it's generally a bad idea to be slow at the beginning.

[vinesthemonkey]

I watched the video and unfortunately I found it very unsatisfying. Anything interesting, beyond the definition of poset, is not explained. It is not clear why the concept of an ordinal makes any sense, or what "too large to be a set" means, or what even the axiom of choice is, or why "well ordering" is justified philosophically

[vinesthemonkey]

you should zoom in on your writing and pictures. right now they are pretty small on mobile

[vinesthemonkey]

Also I think you should pause less when talking. it interrupts the flow