filmov
tv
2^x = 4x

Показать описание
This problem has two solutions. The second solution, if done by algebra will require a special function called the Lambert W function. In my solution, I used a power series approximation to estimate the W(t)
This is the video I mentioned
This is the video I mentioned
2^x = 4x
Viral exponential Equation | 2^x = 4x
A Simple Exponential Equation With a Tricky Solution | 2^x = 4x
Find the value of x || 2^x = 4x || Exponential equation
Confused Equation 😁 | 2^x = 4x
Best Sensitivity For PUBG & BGMI ✅❌ Scope 2x 3x 4x 6x 8x No Recoil Sensitivity 2023 👍 GB ALPHA...
Quadratic Equation: Solve 4x^2 + 2x = 0
Harley-Davidson Cardo Freecom 2x & Freecom 4x Bluetooth Headset Tutorial
Exercise 2.1/Class 8/Maths/Chapter-2/Full Exercise Explained/PSEB/Punjab Board/@PSEBEDUCATE #pseb
Anti-aliasing 2x Vs 4x All Device Enable BGMI 2.7 Update 😱 | Smoth settings Low device bgmi update...
x^2 - 4x + 2 = 0
Linear equation with one unknown: Solve 8-2x=5-4x step-by-step solution
Linear equation with one unknown: Solve 2x=4x-8 step-by-step solution
[YESSS I WIN MOST POPULAR] 20th Century Fox 2x 4x Speed (V2)
The Muffin Song 2x, 4x, 8x Up To 5000x FASTER
Linear equation with one unknown: Solve 5-2x=-4x+9 step-by-step solution
CARDO Freecom 2X / 4X Intercom | FULL Review
BGMI Scope Setting 2x 3x 4x 6x 8x New Best Sensitivity Settings and Controls in 2022
Solve 2x+4=4x: Linear Equation Video Solution | Tiger Algebra
Solve -2x+6+4x=-12: Linear Equation Video Solution | Tiger Algebra
Chrome Dino Speedrunning (2x,4x,8x,16x,32x,64x)
Find (4x - 3y)(2x + 5y)
Linear equation with one unknown: Solve 4x-2(x+3)=8 step-by-step solution
If (x + l)(x + m)=x² + 4x + 2 then the value of l²+m² is
Комментарии
 0:15:34
0:15:34
 0:02:41
0:02:41
 0:11:18
0:11:18
 0:04:37
0:04:37
 0:07:00
0:07:00
 0:01:18
0:01:18
 0:00:37
0:00:37
 0:17:13
0:17:13
 0:18:21
0:18:21
 0:02:52
0:02:52
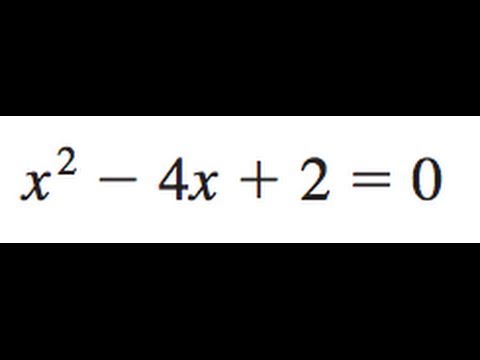 0:00:39
0:00:39
 0:01:21
0:01:21
 0:01:21
0:01:21
 0:02:48
0:02:48
 0:04:00
0:04:00
 0:01:31
0:01:31
 0:12:18
0:12:18
 0:07:26
0:07:26
 0:01:35
0:01:35
 0:01:18
0:01:18
 0:01:03
0:01:03
 0:00:44
0:00:44
 0:01:26
0:01:26
 0:01:56
0:01:56