Row Echelon Form and Reduced Row Echelon Form

Learning Objectives:
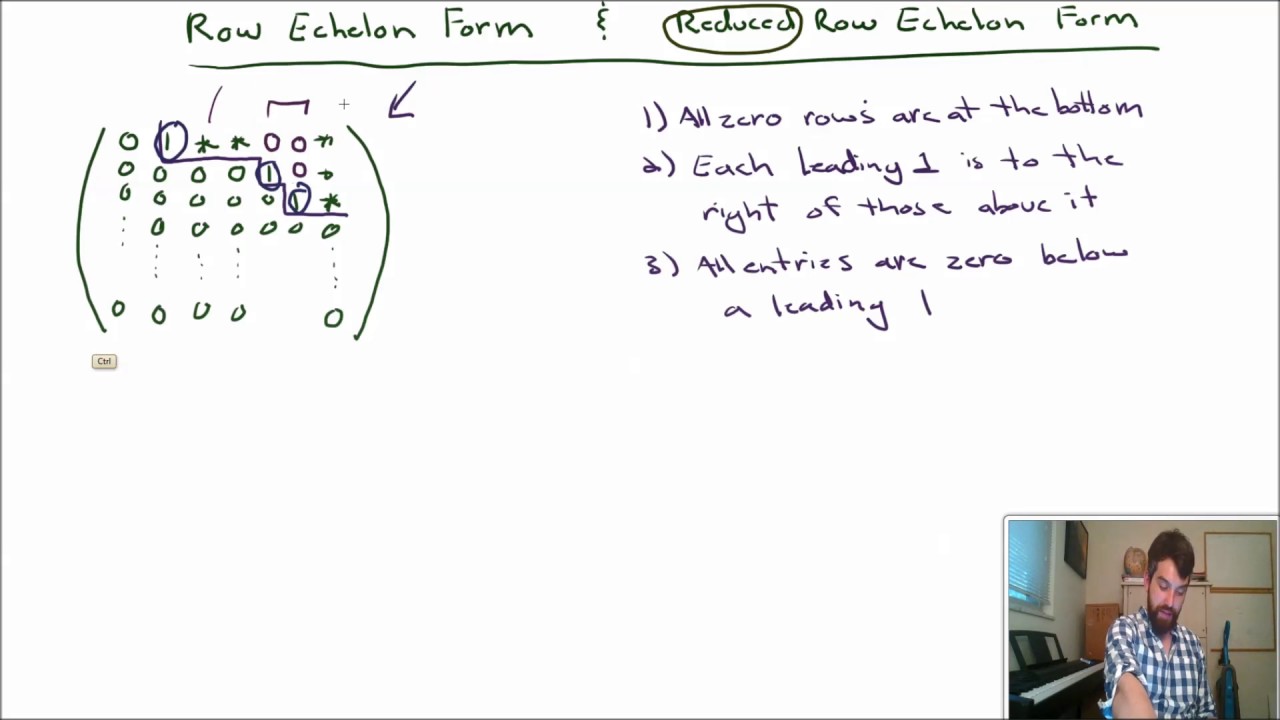
1) Identify the form of REF and RREF visually
2) Write the formal list of conditions to be in REF or RREF
3) Observe the uniqueness of RREF but nonuniqueness of REF

This video is part of a Linear Algebra course taught at the University of Cincinnati.

[dlambert]

This is one of the best linear algebra playlists i have found. Thanks for uploading :)

[mbusombatha]

The day I found you was the day my algebra knowledge came together. thank you

[riwawaves]

thank you so much!! it was through your videos that made linear algebra click for me

[loden]

Really loving this series. Thanks so much!

[eunseohwang]

This helped me a lot! Thank you so much for your content!

[Zephyr-tghu]

Awesome. Thank you so much for making these, Trefor!

[priyanksharma]

Hi, Your lectures on linear algebra are just amazing. Do you also have notes on linear algebra. It would be great if you could share them.

[.melyanaputri]

This is easy to understand. Thank you so much!

[mathadventuress]

zooming before pandemic. youre so awesome.

[dharinibalachandran]

Is it necessary to use only elementary row operations for converting a matrix into a row echelon from, or can we use row and column operations both combined for converting a matrix to REF and RREF?

[ugursoydan]

Are all leading entries of every row of a matrix must be 1 for this matrix to be in row echelon form? Or if the matrices which their leading entries anything other than 1 can also be row echelon form? thank you

[gihanna]

Thank you very much, these are definitely great! I would just suggest to chill the voice a bit :D

[vampyzankar]

Can the asterisk be ones(1) as well? Or they can not be 1 for it to be ref?