filmov
tv
Asymptotics in the complex plane. Asymptotics of Legendre polynomials.
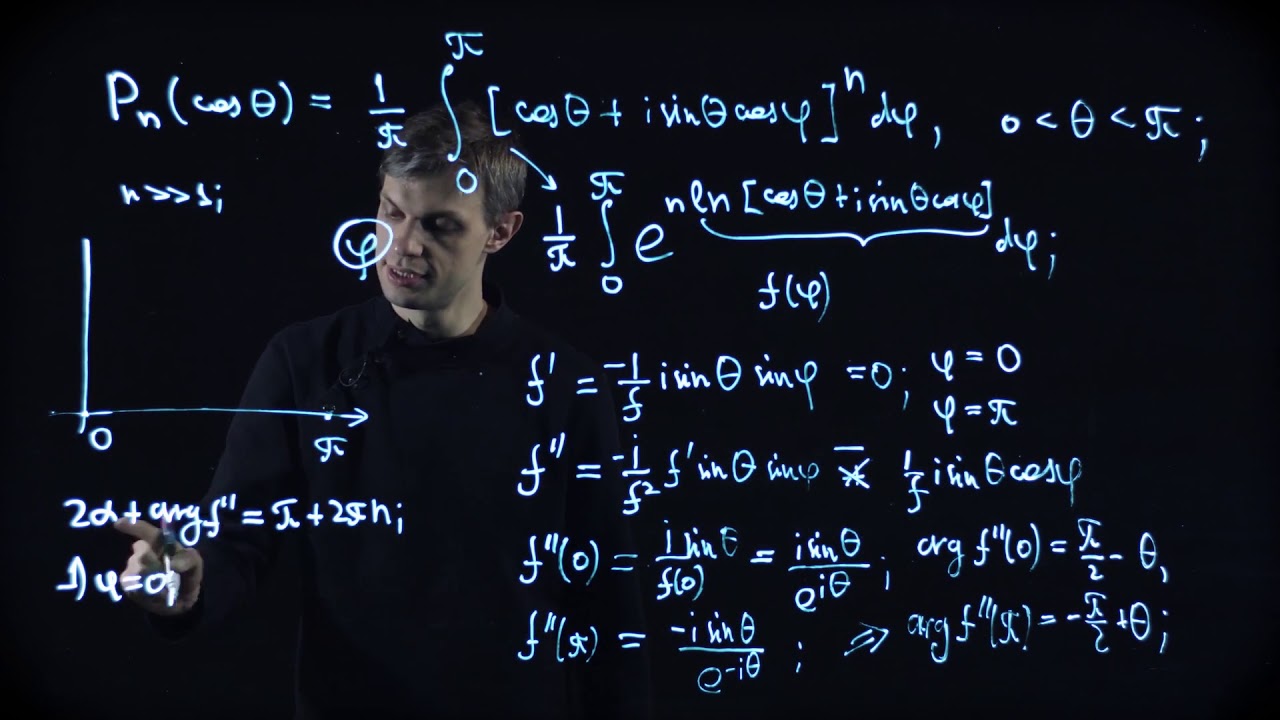
Показать описание
The course is for physics students and reserachers who want to familiarize themselves with the applications of asymptotic complex analysis in Quantum Mechanics and other applied fields.
Topics of the course:
1. Asymptotic series.
2. Special functions.
3. Saddle point approximation with extensive practice.
4. Solution of differential equations with contour integrals.
5. Stokes phenomenon.
6. Related physics applications.
The course is fully operational with more than 50 problems on the edx server (see the link above)
0:11:47
Asymptotics in a complex plane, Taylor Series vs Asymptotic Expansions.
0:07:43
Asymptotics in a complex plane. Stationary phase approximation, Part 1.
0:06:25
Asymptotics in a complex plane, Laplace method, example.
0:08:54
Asymptotics i the complex plane. Digamma function properties and asymptotics, Part 1
0:04:46
Asymptotics in the Complex Plane. Watson's lemma, Part 1
0:10:22
Asymptotics in a complex plane. Stokes phenomenon, Part 4.
0:11:25
Asymptotics in the complex plane. Application of Eulers digamma function, Part 1.
0:21:48
Asymptotics in the complex plane. Asymptotics of Legendre polynomials.
0:08:17
Asymptotics in a complex plane. Hankel representation of the Gamma-function.
0:21:06
Asymptotics in a complex plane. Gamma function, Part 1.
0:13:14
Asymptotics in a complex plane, Taylor Series vs Asymptotic Expansions. Illustration.
0:11:14
Asymptotics in a complex plane. Laplace method, full asymptotic series.
0:15:55
Asymptotics in the complex plane. Computation of infinite products/example I.
0:07:04
Asymptotics in a complex plane, Optimal summation, Superasymptotics.
0:13:58
Asymptotics in a complex plane. Laplace method. Introduction.
0:08:52
Asymptotics in the complex plane. Saddle Point Approximation. Non-homogeneous exponent. P1.
0:10:03
Asymptotics in the complex plane. Relativistic particle in a corner Part 1.
0:10:18
Asymptotics in the complex plane. Solving differential equation with contour integral. Example 1.
0:13:34
Asymptotics in a complex plane. Asymptotic series as approximations of definite integrals.
0:03:54
Asymptotics in a complex plane. Digamma function properties and asymptotics Part 2.
0:13:03
Asymptotics in the complex plane. Saddle Point Approximation. Non-homogeneous exponent. P4.
0:15:41
Asymptotics in the complex plane. Solving differential equation with contour integral. Example 2.P1.
0:05:04
Asymptotics in the complex plane. Solving differential equation with contour integral. P1.
0:12:10
Asymptotics in the complex plane. Application of Eulers digamma function. Part 2.
Комментарии