filmov
tv
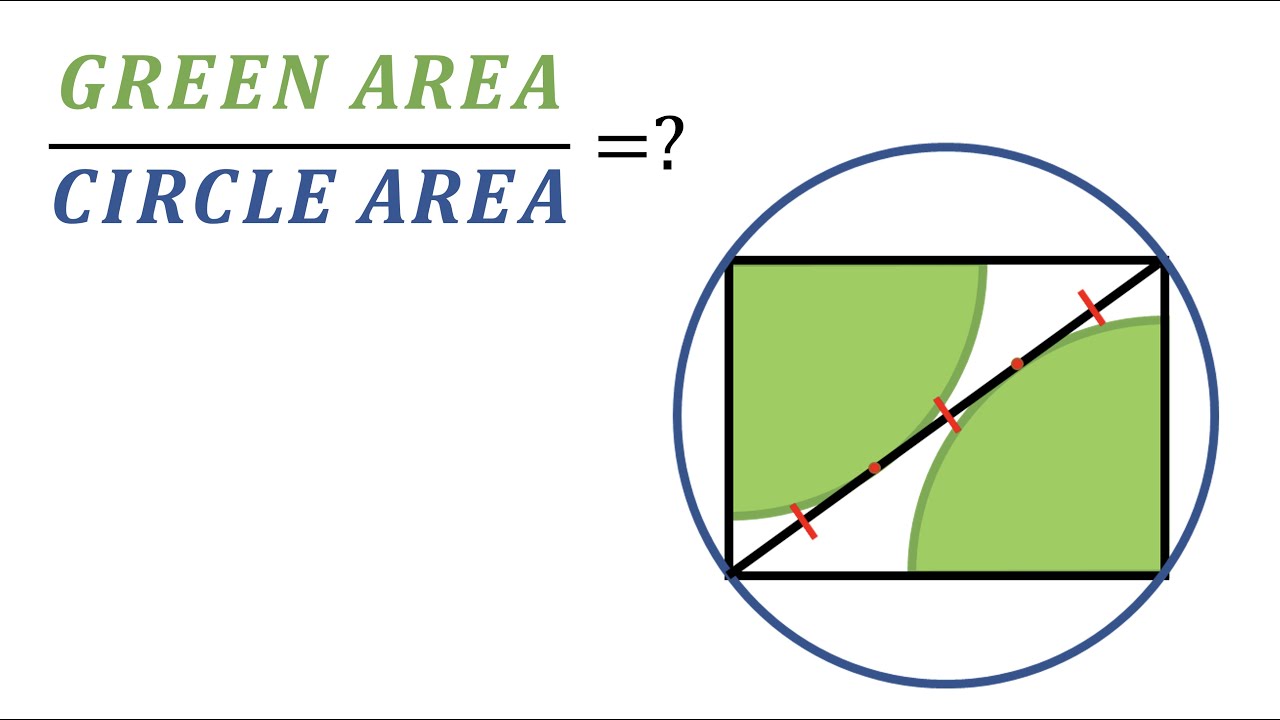
Find ratio of areas in circles and rectangles
Показать описание
Area Ratio
How to Find the Ratio of Areas in a Trapezoid : Math Calculations & More
Find ratio of areas in circles and rectangles
How to Find Ratio of Area in a Square for Shaded Region Challenge Question
Floor Area Ratio Explained by Architect Jorge Fontan
Ratio of Perimeter / Ratio of Area
Find ratio of area of trapezium and triangle AEB in Figure
Ratio of Area of Triangles in a Trapezoid Challenge SAT Question | ACT
💯🔥Find the ratio of areas of two circles//#class10 #shorts #tricks #maths #education Ch-12#ncert#yt...
eMath: Ratio of Areas of Similar Shapes
Ratio of areas of similar triangles
Can you solve this - Ratio of Area of Squares #geometry #maths
How to Find the Ratio of the Perimeter of Two Polygons : Math & Physics Lessons
Ratio of Areas of similar Triangles
CCSS Math - Vectors (Ratio: Triangles with common height)
Find the ratio of length to width of a rectangle. Simplify ratio
6 Ratio of Areas of Triangles in Vectors
Rectangle Dimensions Given as Ratio to Find Possible Length
Ratio of Similar Triangles
Surface Area to Volume Ratio Explained
Ratio of Area of Triangles in Modified Parallelogram Olympiad Challenge
What is the Ratio of perimeters of two squares | Quantitative Ability Problem | FTS | NTS-GATGeneral
Probability By Finding Ratio of Area Triangle Square
Ratio of area of two squares is 1:4. Find ratio of their perimeter.
Комментарии
 0:02:10
0:02:10
 0:03:03
0:03:03
 0:02:46
0:02:46
 0:04:00
0:04:00
 0:04:12
0:04:12
 0:02:38
0:02:38
 0:04:52
0:04:52
 0:10:39
0:10:39
 0:00:40
0:00:40
 0:08:56
0:08:56
 0:03:20
0:03:20
 0:02:37
0:02:37
 0:02:01
0:02:01
 0:01:00
0:01:00
 0:05:53
0:05:53
 0:02:08
0:02:08
 0:06:18
0:06:18
 0:03:04
0:03:04
 0:13:02
0:13:02
 0:03:30
0:03:30
 0:05:34
0:05:34
 0:01:25
0:01:25
 0:05:27
0:05:27
 0:02:23
0:02:23