Problem 13-76 | Force & Acceleration | Chapter: 13 | Kinetics of a Particle

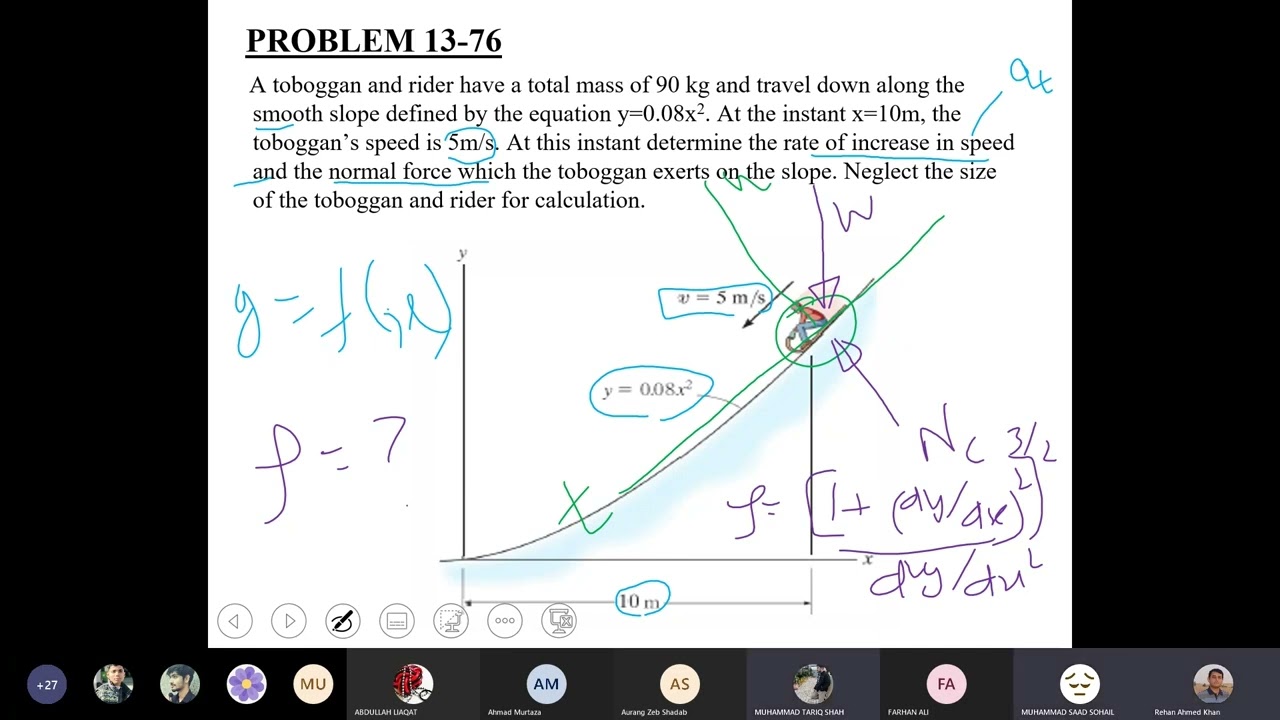
PROBLEM 13-76
A toboggan and rider have a total mass of 90 kg and travel down along the
smooth slope defined by the equation y=0.08x2. At the instant x=10m, the
toboggan’s speed is 5m/s. At this instant determine the rate of increase in speed
and the normal force which the toboggan exerts on the slope. Neglect the size
of the toboggan and rider for calculation.

Welcome to Chapter 13 of "Engineering Mechanics Dynamics," where we delve into the fascinating realm of particle kinetics, specifically focusing on force and acceleration. In this intriguing topic, "Problem 13-76," we encounter a dynamic scenario involving a toboggan and rider descending along a smooth slope defined by a mathematical equation. This scenario presents a unique opportunity to explore the interplay between mass, velocity, and forces in a dynamic context.

📚 Book Name: Engineering Mechanics Dynamics
📝 Chapter: 13 | Kinetics of a Particle

⚙️ Topic: Force & Acceleration Problem 13-76

In this captivating problem, we're presented with a toboggan and rider with a combined mass of 90 kg, traversing down a smooth slope whose profile is defined by the equation y = 0.08x^2. Our objective is twofold: First, we embark on a journey to determine the rate of increase in the toboggan's speed as it moves along the slope. Second, we delve into the dynamics at play to ascertain the normal force exerted by the toboggan on the slope at the precise instant when x = 10 m.

With the tools of physics and engineering at our disposal, we'll harness principles of kinematics, calculus, and dynamics to unlock insights into this scenario. By analyzing the changing speed of the toboggan, we'll uncover the rate at which its velocity is increasing—a key facet of dynamic motion. Simultaneously, we'll explore the normal force exerted by the toboggan on the slope, a force that counteracts gravity and is crucial for maintaining equilibrium and smooth motion.

As we navigate this problem, we'll illuminate the intricate connections between mathematical equations, forces, and motion. By unraveling the mechanics behind this toboggan descent, we'll gain a deeper appreciation for the laws that govern dynamic scenarios and the role they play in real-world applications.

Tags:
#ParticleKinetics, #ForceAndAcceleration, #EngineeringMechanicsDynamics, #DynamicScenario, #TobogganDescent, #KinematicsAndCalculus, #RateOfSpeedIncrease, #NormalForceAnalysis, #EquilibriumInMotion, #MathematicalEquations, #DynamicPhysics, #KinematicPrinciples, #VelocityCalculation, #DynamicForces, #PhysicsInMotion, #KineticDynamics, #DynamicMotion, #AccelerationConcepts, #TobogganPhysics, #DynamicEquilibrium, #SlopeDescent, #TobogganRider, #DynamicApplications, #EquationsAndForces, #DynamicPrinciples, #DynamicsCalculation, #KinematicEquations, #PhysicsAndEngineering, #MotionAnalysis, #DynamicInterplay, #RealWorldDynamics, #PhysicsLaws, #EngineeringInsights, #RateOfIncreaseCalculation, #NormalForcePhysics, #DynamicMath, #TobogganAcceleration, #EngineeringStudies, #DynamicsExploration, #ForceInfluence, #PhysicsAndMotion, #DynamicChallenges, #EquilibriumInPhysics, #TobogganVelocity, #DynamicPhysicsLaws, #AccelerationInfluence, #EngineeringExamples, #DynamicCalculations, #TobogganEquations, #PhysicsPrinciples, #DynamicEquations, #KinematicPhysics