Scalars and Vectors Machine Learning

Welcome to our video on Scalars and Vectors in Machine Learning! In this video, we will explore the concepts of Scalars and Vectors, and how they are used in Machine Learning.

Scalars and Vectors are important mathematical concepts that are used in various fields of study, including physics, engineering, and mathematics. In the field of Machine Learning, Scalars and Vectors are used to represent different types of data.

Scalars:

Scalars are quantities that have only one value, such as temperature, speed, or weight. In Machine Learning, Scalars are used to represent individual data points or features. For example, the age of a person or the number of bedrooms in a house are scalar values.

Scalars are represented using a single number, which can be either a real number or an integer. Scalars are often used as input or output values in Machine Learning algorithms. For example, in a linear regression algorithm, the output value is a scalar that represents the predicted value of a dependent variable.

Vectors:

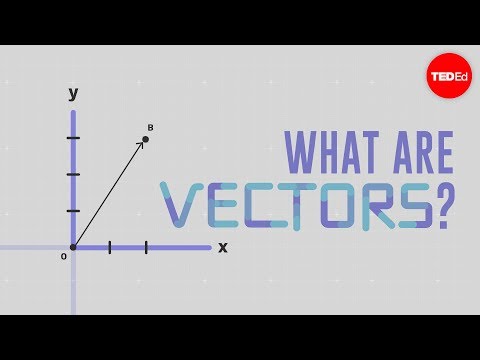
Vectors, on the other hand, are quantities that have both magnitude and direction. In Machine Learning, Vectors are used to represent a collection of scalar values that are related to each other. For example, the pixel values of an image can be represented as a vector.

Vectors are represented using multiple numbers, which are arranged in a specific order. Each number in the vector represents the value of a specific scalar. Vectors are often used as input or output values in Machine Learning algorithms. For example, in a neural network algorithm, the input values are often represented as vectors.

Scalar and Vector Operations:

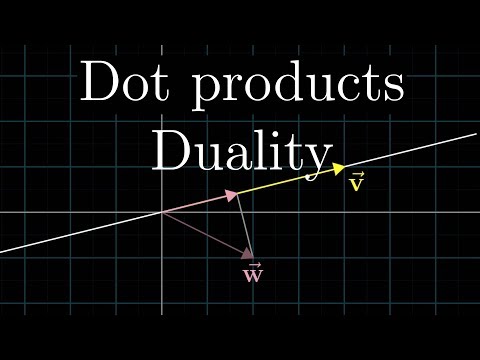
Scalar and Vector operations are important mathematical concepts that are used in Machine Learning. These operations include addition, subtraction, multiplication, and division.

Scalar operations involve applying a scalar value to a scalar or vector value. For example, multiplying a scalar value by a vector value will result in a new vector value that is scaled by the scalar value. In contrast, Vector operations involve applying an operation to two or more vectors. For example, adding two vectors will result in a new vector that is the sum of the two vectors.

Applications of Scalars and Vectors in Machine Learning:

Scalars and Vectors are used in various Machine Learning algorithms. For example, in linear regression algorithms, scalar values are used to represent input features, and the output value is a scalar that represents the predicted value of the dependent variable.

In neural network algorithms, vectors are used to represent input features, and the output value is a vector that represents the predicted values of the dependent variables.

Conclusion:

In conclusion, Scalars and Vectors are important mathematical concepts that are used in Machine Learning. Scalars represent individual data points or features, while Vectors represent a collection of related scalar values. Scalars and Vectors are used in various Machine Learning algorithms, and Scalar and Vector operations are important mathematical concepts that are used in Machine Learning. Understanding Scalars and Vectors is essential for anyone who wants to study Machine Learning. We hope you found this video informative and helpful.

Feature Engineering:
Feature Engineering is the process of selecting and transforming raw data into features that can be used by a Machine Learning algorithm. Scalars and Vectors play a key role in this process. For example, in image recognition tasks, each pixel in an image is a scalar value, and a collection of pixel values can be represented as a vector. By using feature engineering techniques, we can extract important features from an image, such as edges or shapes, and represent them as a vector. This vector can then be used as input to a Machine Learning algorithm.

Dimensionality Reduction:
In some cases, the number of features in a dataset can be very large. This can lead to a phenomenon called the Curse of Dimensionality, where the computational cost of Machine Learning algorithms increases exponentially with the number of features. Dimensionality Reduction is the process of reducing the number of features in a dataset, while preserving the most important information. Scalars and Vectors play a key role in this process. For example, Principal Component Analysis (PCA) is a popular dimensionality reduction technique that involves finding the directions in which the data varies the most, and projecting the data onto these directions. This can be achieved by computing the eigenvectors of the covariance matrix of the data, which can be represented as vectors.