filmov
tv
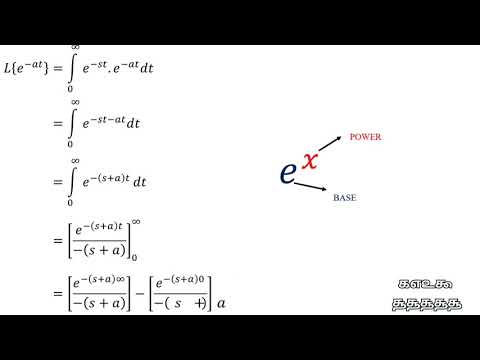
Laplace transform of e^(-at) sinwt
Показать описание
Laplace transform of e^(-at) sinwt
#LaplaceTransformOfe^(-at)sinwt
#LaplaceTransformOfe^(-bt)sinwt
#LaplaceTransformOfe^(-ct)sinwt
#LaplaceTransformOfe^(-dt)sinwt
#LaplaceTransformOfe^(-et)sinwt
#LaplaceTransformOfe^(-ft)sinwt
#LaplaceTransformOfe^(-gt)sinwt
#LaplaceTransformOfe^(-ht)sinwt
#LaplaceTransformOfe^(-it)sinwt
#LaplaceTransformOfe^(-jt)sinwt
#LaplaceTransformOfe^(-kt)sinwt
#LaplaceTransformOfe^(-lt)sinwt
#LaplaceTransformOfe^(-mt)sinwt
#LaplaceTransformOfe^(-nt)sinwt
#LaplaceTransformOfe^(-ot)sinwt
#LaplaceTransformOfe^(-pt)sinwt
#LaplaceTransformOfe^(-qt)sinwt
#LaplaceTransformOfe^(-rt)sinwt
#LaplaceTransformOfe^(-st)sinwt
#LaplaceTransformOfe^(-tt)sinwt
#LaplaceTransformOfe^(-ut)sinwt
#LaplaceTransformOfe^(-vt)sinwt
#LaplaceTransformOfe^(-wt)sinwt
#LaplaceTransformOfe^(-xt)sinwt
#LaplaceTransformOfe^(-yt)sinwt
#LaplaceTransformOfe^(-zt)sinwt
#LaplaceTransformOfe^(-at)sinwt=w/[(a+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-bt)sinwt=w/[(b+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ct)sinwt=w/[(c+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-dt)sinwt=w/[(d+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-et)sinwt=w/[(e+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ft)sinwt=w/[(f+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-gt)sinwt=w/[(g+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ht)sinwt=w/[(h+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-it)sinwt=w/[(i+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-jt)sinwt=w/[(j+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-kt)sinwt=w/[(k+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-lt)sinwt=w/[(l+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-mt)sinwt=w/[(m+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-nt)sinwt=w/[(n+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ot)sinwt=w/[(o+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-pt)sinwt=w/[(p+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-qt)sinwt=w/[(q+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-rt)sinwt=w/[(r+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-st)sinwt=w/[(s+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-tt)sinwt=w/[(t+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ut)sinwt=w/[(u+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-vt)sinwt=w/[(v+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-wt)sinwt=w/[(w+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-xt)sinwt=w/[(x+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-yt)sinwt=w/[(y+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-zt)sinwt=w/[(z+s)^(2)+w^(2)]
#L[e^(-at)sinwt]=w/[(a+s)^(2)+w^(2)]
#L[e^(-bt)sinwt]=w/[(b+s)^(2)+w^(2)]
#L[e^(-ct)sinwt]=w/[(c+s)^(2)+w^(2)]
#L[e^(-dt)sinwt]=w/[(d+s)^(2)+w^(2)]
#L[e^(-et)sinwt]=w/[(e+s)^(2)+w^(2)]
#L[e^(-ft)sinwt]=w/[(f+s)^(2)+w^(2)]
#L[e^(-gt)sinwt]=w/[(g+s)^(2)+w^(2)]
#L[e^(-ht)sinwt]=w/[(h+s)^(2)+w^(2)]
#L[e^(-it)sinwt]=w/[(i+s)^(2)+w^(2)]
#L[e^(-jt)sinwt]=w/[(j+s)^(2)+w^(2)]
#L[e^(-kt)sinwt]=w/[(k+s)^(2)+w^(2)]
#L[e^(-lt)sinwt]=w/[(l+s)^(2)+w^(2)]
#L[e^(-mt)sinwt]=w/[(m+s)^(2)+w^(2)]
#L[e^(-nt)sinwt]=w/[(n+s)^(2)+w^(2)]
#L[e^(-ot)sinwt]=w/[(o+s)^(2)+w^(2)]
#L[e^(-pt)sinwt]=w/[(p+s)^(2)+w^(2)]
#L[e^(-qt)sinwt]=w/[(q+s)^(2)+w^(2)]
#L[e^(-rt)sinwt]=w/[(r+s)^(2)+w^(2)]
#L[e^(-st)sinwt]=w/[(s+s)^(2)+w^(2)]
#L[e^(-tt)sinwt]=w/[(t+s)^(2)+w^(2)]
#L[e^(-ut)sinwt]=w/[(u+s)^(2)+w^(2)]
#L[e^(-vt)sinwt]=w/[(v+s)^(2)+w^(2)]
#L[e^(-wt)sinwt]=w/[(w+s)^(2)+w^(2)]
#L[e^(-xt)sinwt]=w/[(x+s)^(2)+w^(2)]
#L[e^(-yt)sinwt]=w/[(y+s)^(2)+w^(2)]
#L[e^(-zt)sinwt]=w/[(z+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-at)sinwt
#LaplaceTransformOfe^(-bt)sinwt
#LaplaceTransformOfe^(-ct)sinwt
#LaplaceTransformOfe^(-dt)sinwt
#LaplaceTransformOfe^(-et)sinwt
#LaplaceTransformOfe^(-ft)sinwt
#LaplaceTransformOfe^(-gt)sinwt
#LaplaceTransformOfe^(-ht)sinwt
#LaplaceTransformOfe^(-it)sinwt
#LaplaceTransformOfe^(-jt)sinwt
#LaplaceTransformOfe^(-kt)sinwt
#LaplaceTransformOfe^(-lt)sinwt
#LaplaceTransformOfe^(-mt)sinwt
#LaplaceTransformOfe^(-nt)sinwt
#LaplaceTransformOfe^(-ot)sinwt
#LaplaceTransformOfe^(-pt)sinwt
#LaplaceTransformOfe^(-qt)sinwt
#LaplaceTransformOfe^(-rt)sinwt
#LaplaceTransformOfe^(-st)sinwt
#LaplaceTransformOfe^(-tt)sinwt
#LaplaceTransformOfe^(-ut)sinwt
#LaplaceTransformOfe^(-vt)sinwt
#LaplaceTransformOfe^(-wt)sinwt
#LaplaceTransformOfe^(-xt)sinwt
#LaplaceTransformOfe^(-yt)sinwt
#LaplaceTransformOfe^(-zt)sinwt
#LaplaceTransformOfe^(-at)sinwt=w/[(a+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-bt)sinwt=w/[(b+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ct)sinwt=w/[(c+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-dt)sinwt=w/[(d+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-et)sinwt=w/[(e+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ft)sinwt=w/[(f+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-gt)sinwt=w/[(g+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ht)sinwt=w/[(h+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-it)sinwt=w/[(i+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-jt)sinwt=w/[(j+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-kt)sinwt=w/[(k+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-lt)sinwt=w/[(l+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-mt)sinwt=w/[(m+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-nt)sinwt=w/[(n+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ot)sinwt=w/[(o+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-pt)sinwt=w/[(p+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-qt)sinwt=w/[(q+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-rt)sinwt=w/[(r+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-st)sinwt=w/[(s+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-tt)sinwt=w/[(t+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-ut)sinwt=w/[(u+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-vt)sinwt=w/[(v+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-wt)sinwt=w/[(w+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-xt)sinwt=w/[(x+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-yt)sinwt=w/[(y+s)^(2)+w^(2)]
#LaplaceTransformOfe^(-zt)sinwt=w/[(z+s)^(2)+w^(2)]
#L[e^(-at)sinwt]=w/[(a+s)^(2)+w^(2)]
#L[e^(-bt)sinwt]=w/[(b+s)^(2)+w^(2)]
#L[e^(-ct)sinwt]=w/[(c+s)^(2)+w^(2)]
#L[e^(-dt)sinwt]=w/[(d+s)^(2)+w^(2)]
#L[e^(-et)sinwt]=w/[(e+s)^(2)+w^(2)]
#L[e^(-ft)sinwt]=w/[(f+s)^(2)+w^(2)]
#L[e^(-gt)sinwt]=w/[(g+s)^(2)+w^(2)]
#L[e^(-ht)sinwt]=w/[(h+s)^(2)+w^(2)]
#L[e^(-it)sinwt]=w/[(i+s)^(2)+w^(2)]
#L[e^(-jt)sinwt]=w/[(j+s)^(2)+w^(2)]
#L[e^(-kt)sinwt]=w/[(k+s)^(2)+w^(2)]
#L[e^(-lt)sinwt]=w/[(l+s)^(2)+w^(2)]
#L[e^(-mt)sinwt]=w/[(m+s)^(2)+w^(2)]
#L[e^(-nt)sinwt]=w/[(n+s)^(2)+w^(2)]
#L[e^(-ot)sinwt]=w/[(o+s)^(2)+w^(2)]
#L[e^(-pt)sinwt]=w/[(p+s)^(2)+w^(2)]
#L[e^(-qt)sinwt]=w/[(q+s)^(2)+w^(2)]
#L[e^(-rt)sinwt]=w/[(r+s)^(2)+w^(2)]
#L[e^(-st)sinwt]=w/[(s+s)^(2)+w^(2)]
#L[e^(-tt)sinwt]=w/[(t+s)^(2)+w^(2)]
#L[e^(-ut)sinwt]=w/[(u+s)^(2)+w^(2)]
#L[e^(-vt)sinwt]=w/[(v+s)^(2)+w^(2)]
#L[e^(-wt)sinwt]=w/[(w+s)^(2)+w^(2)]
#L[e^(-xt)sinwt]=w/[(x+s)^(2)+w^(2)]
#L[e^(-yt)sinwt]=w/[(y+s)^(2)+w^(2)]
#L[e^(-zt)sinwt]=w/[(z+s)^(2)+w^(2)]
0:11:43
Laplace transform of e^(-at) sinwt
0:13:19
Laplace transform of e^(at)sinwt
0:14:02
Laplace Transform of e^(at) sin(wt) and e^(at) cos(wt)
0:07:10
Electrical Engineering: Ch 16: Laplace Transform (7 of 58) Laplace Transform of f(t)=cos(wt)e^(at)
0:08:53
7.1-15 Find Laplace Transform of (e^-t)sint | DE
0:08:28
2 7 Laplace Transforms of an Exponential and a Sinusoidal - Differential Equations
0:04:02
Laplace Transform of e to the power at sin bt @derivewithsoumya
0:02:18
Laplace Transform of e^(2t)sin(3t)
0:15:47
Laplace transform of sin(bt), using definition and integration by parts
0:06:28
Electrical Engineering: Ch 16: Laplace Transform (6 of 58) The Laplace Transform of f(t)=sin(wt)
0:06:48
Laplace Transform of Basic Signals [Sinω₀t.u(t)]
0:08:11
The Laplace transform.of f(t)=sin(t)
0:01:45
Laplace Transform of e^(3t)sin(4t)
0:11:40
Laplace Transform of Basic Signals [Cosω₀t.u(t)]
0:00:17
Laplace Transform of e^(4t) #shorts
0:04:18
Laplace Transform of e^-t [Integral from 0 to t of Sint/t]
0:09:20
Find the Laplace transform of the sine function (Laplace transform of sin(t)).
0:09:51
Laplace Transform - Example (f(t) = e^t*sin(t))
0:00:31
laplace transform of t^n*e^(at)*sin(bt)
0:08:08
Engg_Maths | Find The Laplace Transform Of The Following Functions [e^(t-1) + sin (t-1)] u (t-1)
0:00:15
Laplace Transform of t^4 #shorts
0:12:21
Laplace transform of e^(at)coswt
0:01:46
How to use the Convolution Theorem to Find the Laplace Transform of a Convolution EX e^(2t)*sin(t)
0:01:36
Laplace transform of e power minus a t | L{e^-at} | L{e^at}| in English
Комментарии