filmov
tv
Solving System of differential equation by diagonalizing a matrix, Dr. Peyam's Show

Показать описание
Solving System of differential equation by diagonalizing a matrix,
by Dr. Peyam Tabrizian,
system of equations and linear algebra,
blackpenredpen
by Dr. Peyam Tabrizian,
system of equations and linear algebra,
blackpenredpen
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
System of differential equations by elimination, ex1
How to solve differential equations
8: Eigenvalue Method for Systems - Dissecting Differential Equations
Solving System of Differential equations with initial condition
System of differential equations by elimination, sect5.2#9
Coupled System of Differential Equations
Matrix Systems of Differential Equations
10th Class Mathematics, Chapter 1, Exercise 1.1, Question 2 Part 4 | M.I MATHEMATICS@m.imathematics
Differential equations, a tourist's guide | DE1
Homogeneous Systems of Linear Equations - Intro to Eigenvalue/Eigenvector Method
How to solve systems of differential equations
Differential Equations | Solving a system of differential equations with the Laplace transform.
Differential Equations - Systems of Equations (Elimination Method)
Solving Systems of Differential Equations with Eigenvalues and Eigenvectors
Solving Systems of Equations By Elimination & Substitution With 2 Variables
This is why you're learning differential equations
Solving System of differential equation by diagonalizing a matrix, Dr. Peyam's Show
First Order Linear Differential Equations
the outstanding Laplace method for solving systems of ode
Differential equation introduction | First order differential equations | Khan Academy
Solving a System of Differential Equations using Laplace Transforms
How to Solve Differential Equations in PYTHON
First Order Linear Differential Equation & Integrating Factor (introduction & example)
Комментарии
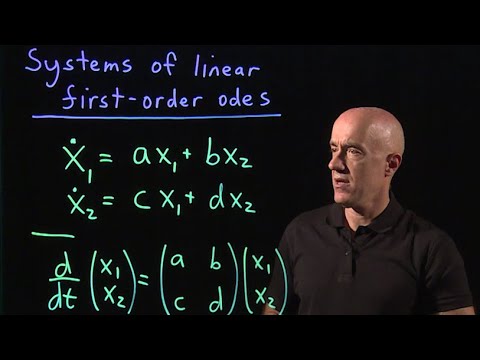 0:08:28
0:08:28
 0:20:44
0:20:44
 0:00:46
0:00:46
 0:08:57
0:08:57
 0:04:46
0:04:46
 0:17:23
0:17:23
 0:07:19
0:07:19
 0:24:58
0:24:58
 0:00:47
0:00:47
 0:27:16
0:27:16
 0:18:44
0:18:44
 0:11:50
0:11:50
 0:07:07
0:07:07
 0:15:40
0:15:40
 0:21:51
0:21:51
 0:10:27
0:10:27
 0:18:36
0:18:36
 0:08:29
0:08:29
 0:22:28
0:22:28
 0:08:29
0:08:29
 0:07:49
0:07:49
 0:13:47
0:13:47
 0:23:37
0:23:37
 0:20:34
0:20:34