filmov
tv
Logarithmic Inequality (fractional base)

Показать описание
In this video I highlighted a common mistake students make in solving this kind of logarithmic inequality
Logarithmic Inequality (fractional base)
Variable Base Logarithmic Inequality, log base x^3 (x-4) strictly less than 1/6
Amazing Logarithmic Inequality
Solving Logarithmic Inequalities | General Mathematics
Solving Logarithmic Inequalities (Worked Example)
Evaluating a Logarithm With a Fraction Base
Fraction comparison involving logarithms - Exam practice.
Solving logarithmic Inequalities
Solving Logarithmic Inequalities (Senior High School General Mathematics 11 MELC - Based)
Solving Log Equation
Logarithmic Inequalities
Logarithmic inequalities with a variable base : Lecture 10 : log(x)(4x+5)/(6-5x) less than -1
Logarithms 5 - Logarithmic Inequalities
Basic Examples in Solving Logarithmic Inequalities
Precalculus Algebra 6.5.4 Exponential and Logarithmic Inequalities
How to Solve Exponential Equation with Fractional Bases - Simple Tips and Tricks
Logarithmic Form to Exponential Form 🤯 #Shorts #algebra #math #maths #mathematics #education #learn...
Logarithmic inequalities explained.
Solving Logarithmic Inequalities made easy, General mathematics
Solving Logarithmic Inequalities (The Basics)
Solving Exponential Equation
An interesting Logarithmic Inequality
Video Lecture for Exponential and Logarithmic Equations/Inequalities
Exponential and Logarithmic Inequalities - Mathematics T Semester 1
Комментарии
 0:10:03
0:10:03
 0:04:32
0:04:32
 0:03:54
0:03:54
 0:11:22
0:11:22
 0:10:39
0:10:39
 0:01:53
0:01:53
 0:00:24
0:00:24
 0:19:41
0:19:41
 0:22:37
0:22:37
 0:00:55
0:00:55
 0:13:08
0:13:08
 0:06:25
0:06:25
 0:32:09
0:32:09
 0:13:03
0:13:03
 0:08:10
0:08:10
 0:06:17
0:06:17
 0:00:14
0:00:14
 0:09:32
0:09:32
 0:31:07
0:31:07
 0:22:44
0:22:44
 0:00:56
0:00:56
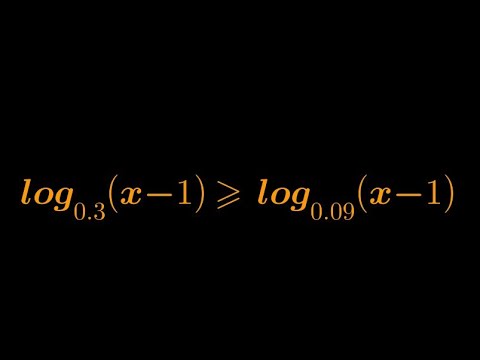 0:05:13
0:05:13
 1:33:14
1:33:14
 0:32:17
0:32:17