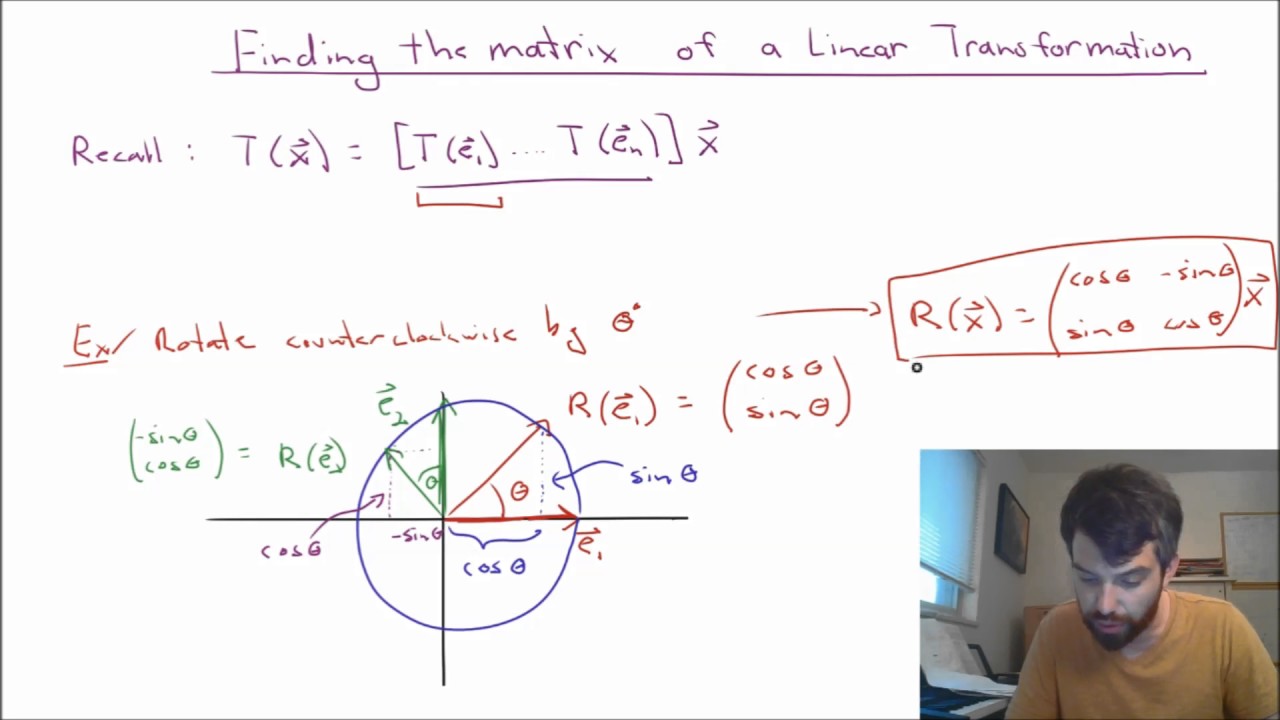
Finding the Matrix of a Linear Transformation

Показать описание

Learning Objectives:
1) Given some linear transformation, find it's matrix.
2) Describe in particular the classic Rotation Matrix.

This video is part of a Linear Algebra course taught at the University of Cincinnati.

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

Рекомендации по теме

Комментарии

Sir, your clarity of mind is giving me Mathematics Enlightenment

sagaraliasjackey

11 months have passed and I'm back for more. Love these series

kolo

For me Linear Algebra = Span {Dr. Trefor Bazzett, Blue and Brown}

SocratesAlexander

This what I was waiting for ( to know how can we rotate a vector using linear transformation ) . Satisfied now 🤭🤭 . I taught it would be more complex but it ain't was .thank you sir ❤️❤️

sudarshann

Holy crap that was beautiful. Eyes have been opened, worlds have been exploded. Thank you!

jacobm

Sir...instead of clockwise flipping, can't we flip the vector e2 over y=x in counter-clockwise direction and then rotate 90° clockwise?

sumittete

your explanation crystal clear thank you

radwanalaghawani

Hi Trefor, Great stuff all around. But I think you may want to check your angle for R(e2), yes? You rotate e2 theta degrees from the Y axis, so sin and cos of R(e2) wouldn't use theta... Just a friendly observation is you get back to this video. Thanks for what you do!

uforreel

Would this be in my first linear algebra class or is this more advanced that that?

wjrasmussen

Hi Professor, I have problem in understanding about how you came up with sine theta and cos theta as the vertical component and the horizontal component respectively for e1.

It definitely looks like a right angled triangle. So, sine theta is opposite / Hypotenuse. If we need to conclude opposite side of the triangle as sin theta, which was from the rotation of e1, we need to know that the hypotenuse must be 1 right ? Could you please explain a bit deeper on that ?

kathirs

This only works for domain R2 -> co-domain R2, correct?

ryanjacksonx

Finding the Matrix of a Linear Transformation

How to Find the Matrix of a Linear Transformation

Solving Matrix Equations

Finding the Matrix of a Linear Transformation

Evaluating the Determinant of a Matrix

How to Find the Rank of a Matrix (with echelon form) | Linear Algebra

Standard Matrix - Full Example Explained

Inverse of a 3x3 Matrix

Trick for finding the the determinant of a Matrix

Finding Basis for the Column Space of a Matrix | Linear Algebra

How To Find The Determinant of a 3x3 Matrix

The rank of a matrix

Finding and using the matrix of a linear transformation relative to non standard bases

Inverse Matrices and Their Properties

Find Null Space and Nullity of a Matrix | Linear Algebra

Find a Transformation Matrix (Standard Matrix) Given a Matrix Transformation: R3 to R3

Transformation matrix with respect to a basis | Linear Algebra | Khan Academy

Matrix with respect to a basis

Example of finding matrix inverse | Matrix transformations | Linear Algebra | Khan Academy

Linear Algebra ||1.5 Elementary Matrix and a Method for finding A Inverse.

Example of Finding the Coefficient Matrix of a System of Linear Equations

How To Find The Cofactors Of A Matrix

How to find the range of a matrix: example

Find Standard Matrix for Linear Transformation | Linear Algebra Exercises

Robotics 2 U1 (Kinematics) S3 (Jacobian Matrix) P2 (Finding the Jacobian)