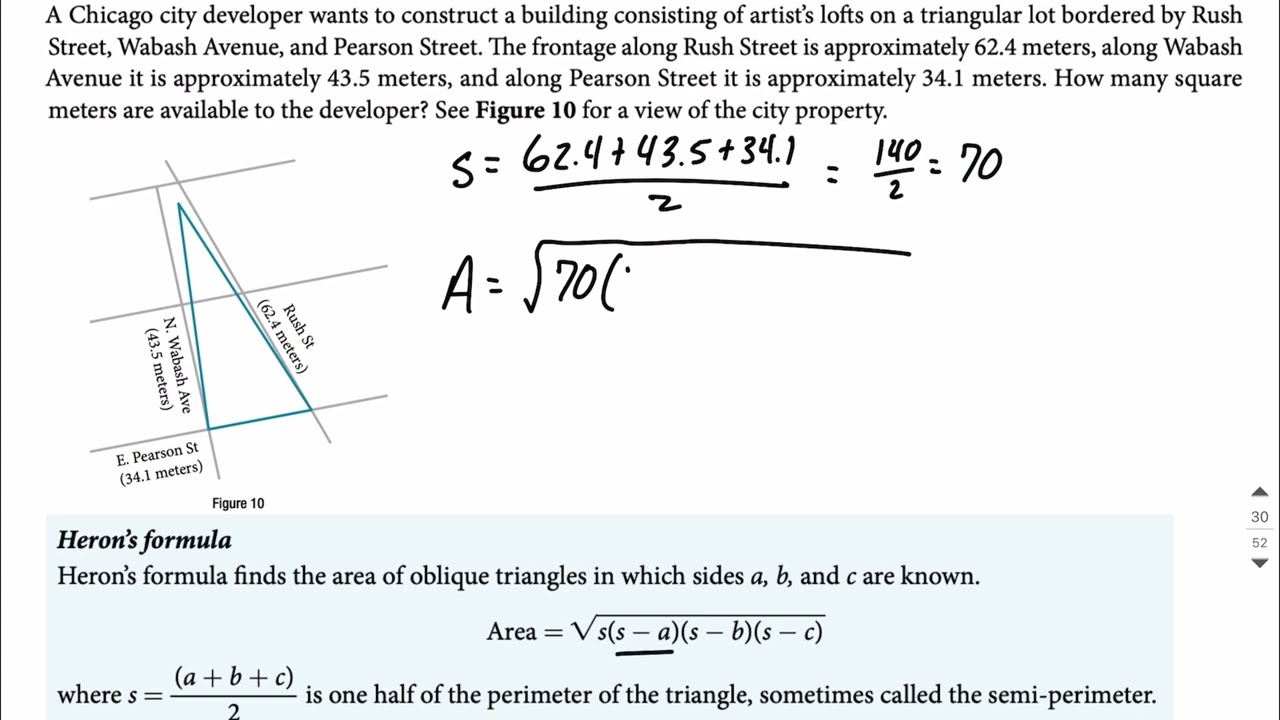
Finding area of triangular lot by using frontage measurements

In this math example, we are trying to find the area of a triangle but it is not as simple as filling into the triangle area formula 1/2(base)(height) because we are not given the height. Instead, we must use Heron's formula. To do so, we first find the semi-perimeter by adding together all three side lengths and dividing the result by 2. We then show all the work to use our semi-perimeter and side lengths to fill in and simplify down. The result is the area of the triangle.

I personally find this to be a very interesting and useful formula because we are not always given both the height and base for a triangle to find an area. This real-life example does a good job of putting such an example together that is accessible to visualize such a situation.

A Chicago city developer wants to construct a building consisting of artist's lofts on a triangular lot bordered by Rush Street, Wabash Avenue, and Pearson Street. The frontage along Rush Street is approximately 62.4 meters, along Wabash Avenue it is approximately 43.5 meters, and along Pearson Street it is approximately 34.1 meters. How many square meters are available to the developer?