filmov
tv
Comparison: Number of Puzzle Permutations

Показать описание
How many different scrambles does each Rubik's Cube puzzle have? This is a comparison video of how many different permutations that different types of twisty puzzles have...
Some sources I used:
Music: Icelandic Arpeggios by DivKid
✨I'm sponsored by TheCubicle!✨
🤑Use code "Rowan" for 5% off your order!
#TeamCubicle
Some sources I used:
Music: Icelandic Arpeggios by DivKid
✨I'm sponsored by TheCubicle!✨
🤑Use code "Rowan" for 5% off your order!
#TeamCubicle
Comparison: Number of Puzzle Permutations
Comparison: How Many Permutations?
The Infinite Combinations Of The 19x19 Rubik’s Cube
Comparison: Hardest Rubik's cube methods to learn
Comparison: Twisty Puzzle Permutations
Why Are There 43,252,003,274,489,856,000 Rubik's Cube Combinations?
How Many Permutations Does Each Puzzle Have? 🤩😮 #rubikscube #speedcubing #comparison #cubing #shorts...
How many permutations? (Part 2)
How many permutations? (Part 1)
How many permutations in a 2x2 rubik's cube #jperm
Comparison: Are You as Fast as the Average Speedcuber?
Permutations of a 17x17 Rubik's Cube!?
How to Calculate Permutations on ANY nxn Rubik's Cube (examples, formula, code)
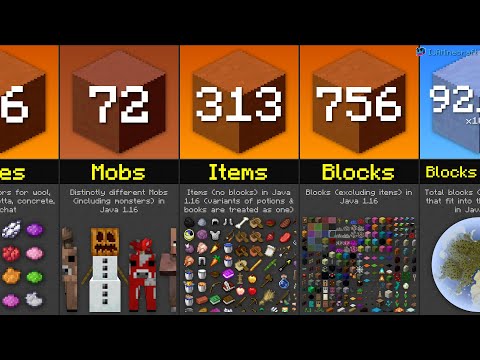
Minecraft Numbers Comparison (2020)
Permutations Puzzle for Maths at Home
Permutations & Combinations | Learn In 60 Seconds | As Usual, JEE Content Like Never Before #sho...
How to Calculate the Permutations of a Rubik's Cube
how to calculate permutations on a 2x2.(tips and tricks)
Paths Across a Grid (Permutations & Combinations)
R Permutations
How to do a 4D Puzzle Rotation
Introduction to Circular Arrangements
Derangements: A Permutations Puzzle
[Continuum EP2] Finding The Number of Permutations on The Rubik's Cube
Комментарии
 0:01:59
0:01:59
 0:00:29
0:00:29
 0:06:41
0:06:41
 0:01:38
0:01:38
 0:00:47
0:00:47
 0:06:54
0:06:54
 0:00:45
0:00:45
 0:00:09
0:00:09
 0:00:12
0:00:12
 0:02:17
0:02:17
 0:01:22
0:01:22
 0:00:14
0:00:14
 0:15:53
0:15:53
 0:03:08
0:03:08
 0:05:35
0:05:35
 0:01:00
0:01:00
 0:09:35
0:09:35
 0:05:02
0:05:02
 0:11:06
0:11:06
 0:04:36
0:04:36
 0:00:31
0:00:31
 0:06:10
0:06:10
 0:05:00
0:05:00
![[Continuum EP2] Finding](https://i.ytimg.com/vi/6q78GythbzY/hqdefault.jpg) 0:17:37
0:17:37