Point of Inflection - Point of Inflexion - f''(x)=0 - Definition - How to Find - Worked Example 1

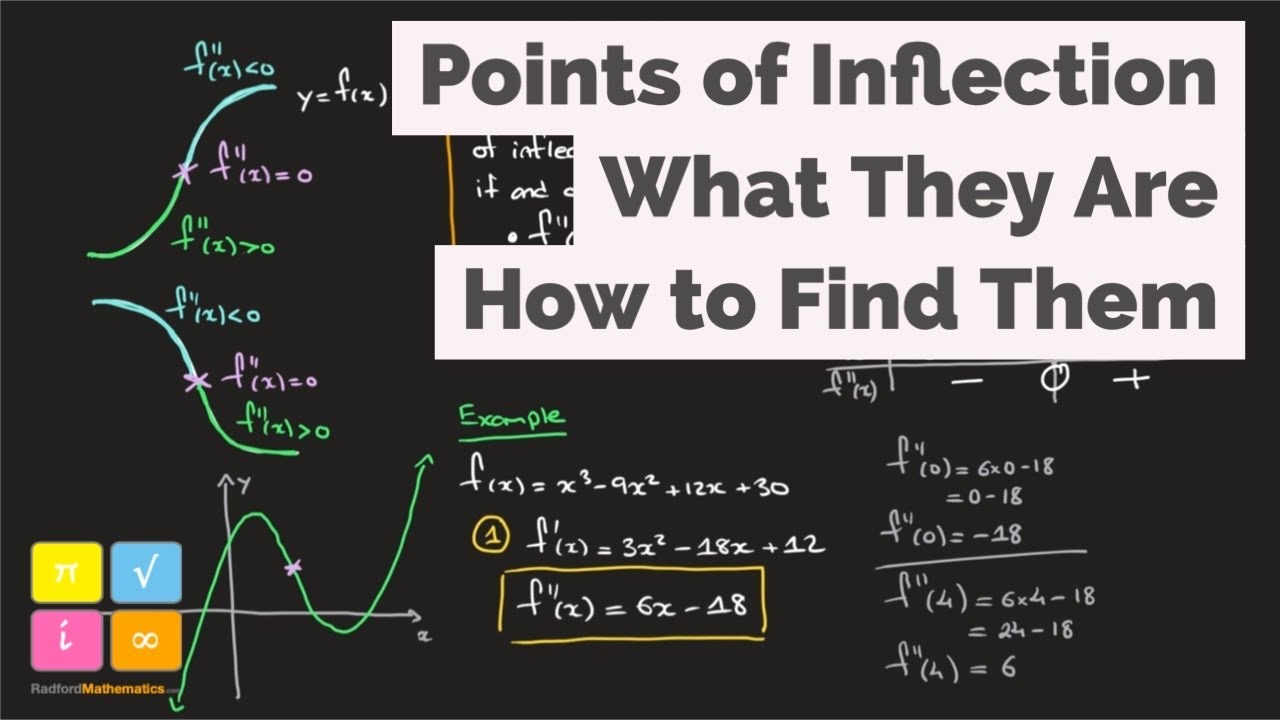
A point of inflection, or inflexion, is a point at which a curve’s concavity changes, either from concave down to concave up, or from concave up to concave down. The second derivative, f’’(x), equals to zero at a point of inflection and its sign changes as we move across one.
In this video I explain what a point of inflection is and I show how to find a point of inflection, with a three-step method.

******** TIMESTAMPS / CHAPTERS ********

00:00 Introduction
00:27 Point of Inflection Definition
03:07 How to Find a Point of Inflection (step 1 and 2)
05:14 f’’(x)=0 a Necessary but Not Sufficient Condition for a Point of Inflection
06:25 Checking sign change of f’’(x) with a sign table (step 3)

[gabbystudyschool]

Thank you sir 🙏🏻🙏🏻
your video is very useful👍🏻👍🏻

[jiraiya]

May u tell me sir, how do we check f"x less than Or greater than zero from graph like u did in this lecture

[jiraiya]

Sir, can u tell how to check when f"x<0 or greater than zero on graph from its slope?
Actually I forgot so I'm searching down the net came across this video
I searched "does sign changes at poi like it's necessary "