filmov
tv
The Finite Difference Method (2D)

Показать описание
The Finite Difference Method for 2D linear differential equations
in which I introduced the finite difference method for solving 1D linear ODEs.
I show how a 2D problem which naturally leads to a 3D matrix can be reduced to a 1D problem leading to a 2D matrix.
Once the problem is expressed as a 2D matrix, it is almost trivial to solve.
in which I introduced the finite difference method for solving 1D linear ODEs.
I show how a 2D problem which naturally leads to a 3D matrix can be reduced to a 1D problem leading to a 2D matrix.
Once the problem is expressed as a 2D matrix, it is almost trivial to solve.
The Finite Difference Method (2D)
MIT Numerical Methods for PDE Lecture 3: Finite Difference for 2D Poisson's equation
Finite Differences
Solving 2D wave quation (Finite difference method) II
Finite Difference Method: 2D Heat Equation with FTCS Scheme
Solving for two-dimensional temperature profiles using the finite difference approximation and Excel
Solve 2D Transient Heat Conduction Problem in Cylindrical Coordinates - Finite Difference Method
10-4 Finite difference method in 2D
MEGR3116 Chapter 4.4 Two Dimensional Steady State Conduction: Finite Difference Equations
Lecture -- Introduction to Two-Dimensional Finite-Difference Method
Solving 2D wave quation (Finite difference method)
Numerical Solution of 2D Laplace equation using Finite Difference Method (Iterative Technique )
CMPSC/Math 451. April 22, 2015. Laplace Equation in 2D. Finite Difference Method. Wen Shen
2D Acoustic wave equation with finite differences
CFD Course - 19 - Finite Difference Method: 2D case
Heat Transfer L11 p3 - Finite Difference Method
MIT Numerical Methods for PDE Lecture 3: Finite Difference 2D Matlab Demo
Solving The 1D & 2D Heat Equation Numerically in Python || FDM Simulation - Python Tutorial #4
Heat Transfer (12): Finite difference examples
Heat Transfer (14) | Chapter 04 | Example | Finite difference 2D
The Finite Difference Method (1D)
Lecture 13 02 Elliptic PDEs - Finite difference method
Finite Difference Methods for 2D and 3D Problems
Finite Difference Method for 2D Circular Membrane 2 (Cylindrical Polar Wave Equation)
Комментарии
 0:15:42
0:15:42
 0:13:21
0:13:21
 0:08:35
0:08:35
 0:00:22
0:00:22
 0:03:11
0:03:11
 0:30:01
0:30:01
 0:26:37
0:26:37
 0:14:12
0:14:12
 0:09:06
0:09:06
 0:13:29
0:13:29
 0:00:21
0:00:21
 0:44:56
0:44:56
 0:52:00
0:52:00
 0:06:43
0:06:43
 0:17:01
0:17:01
 0:10:28
0:10:28
 0:06:20
0:06:20
 0:10:48
0:10:48
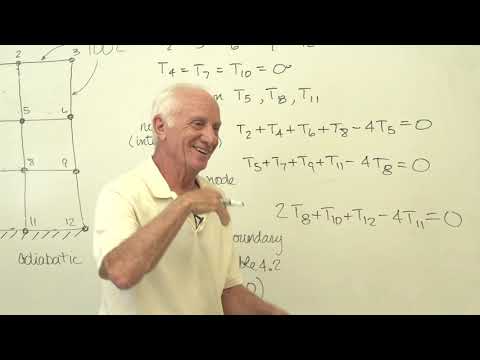 0:46:42
0:46:42
 0:27:43
0:27:43
 0:23:18
0:23:18
 0:08:26
0:08:26
 0:09:38
0:09:38
 0:00:26
0:00:26