filmov
tv
Changing Order of a Double Summation
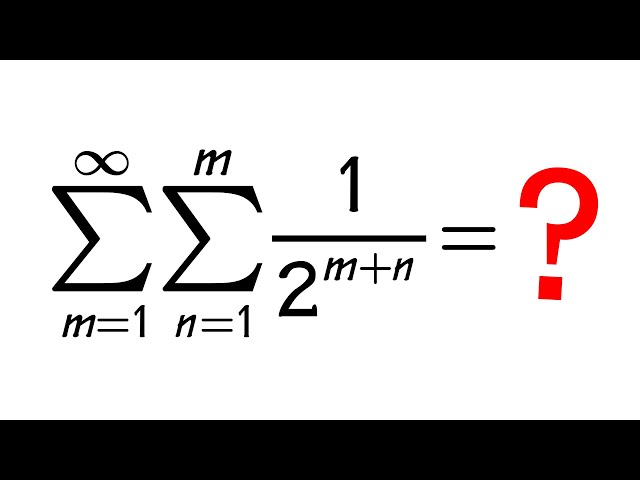
Показать описание
My Game Changers!
Check out my site & social media
blackpenredpen
100/(1-x)
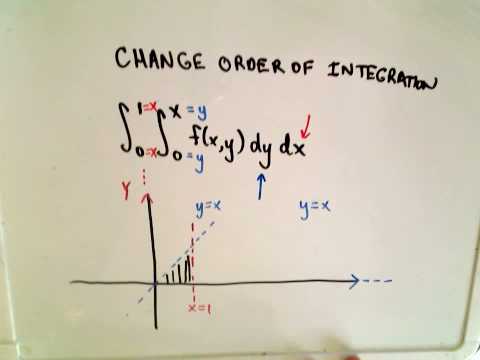
How to change the order of a double integral
❖ Double Integrals - Changing Order of Integration ❖
Changing Order of a Double Summation
❖ Double Integrals - Changing Order of Integration - Full Ex. ❖
Changing the order of double integral in under one minute
Double Integrals: Changing Order of Integration
how to change the order of a double integral (from dydx to dxdy)
a classic double integral that you have to change the order first!
evaluating a double integral, quick and easy (but change the order first!)
How to evaluate double integrals (& how to change the order of integration) 10 examples, calculu...
Double Integrals: Changing the Order of Integration - Example 1
Double Integrals: Changing the Order of Integration
Changing the Order of Integration (Double Integrals)
Double integral change order example
Changing the Order of Double Integral sin(y^2)
Double Integration - Change of Order of Integration | Cartesian & Polar
Harder Double Integrals by Changing Order of Integration (Fubini's Thm) [Ex. 1/4] | Double Inte...
Double Integrals: Changing the Order of Integration - Example 2
Change the Order of Integration | Numericals | Double Integration | Maths 1
Ex: Evaluate a Double Integral to Determine Volume - Change Order of Integration
Double Integrals Changing order of integration
Double integral which requires order of integration change
Double Integrals Changing Order - 2 Detailed Examples
changing the order of double integral from dydx to dxdy
Комментарии
 0:11:12
0:11:12
 0:04:20
0:04:20
 0:08:56
0:08:56
 0:08:36
0:08:36
 0:00:54
0:00:54
 0:02:10
0:02:10
 0:07:14
0:07:14
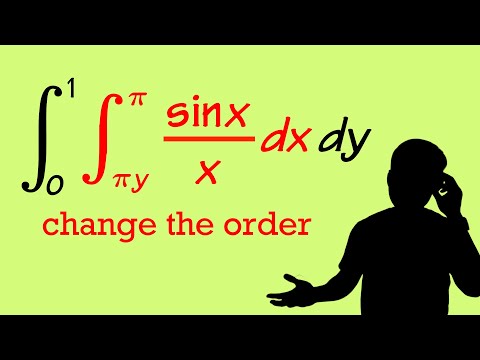 0:04:56
0:04:56
 0:04:29
0:04:29
 0:34:53
0:34:53
 0:05:01
0:05:01
 0:08:36
0:08:36
 0:18:36
0:18:36
 0:08:23
0:08:23
 0:05:23
0:05:23
 0:22:10
0:22:10
 0:12:39
0:12:39
 0:05:47
0:05:47
 0:19:19
0:19:19
 0:07:38
0:07:38
 0:12:15
0:12:15
 0:09:37
0:09:37
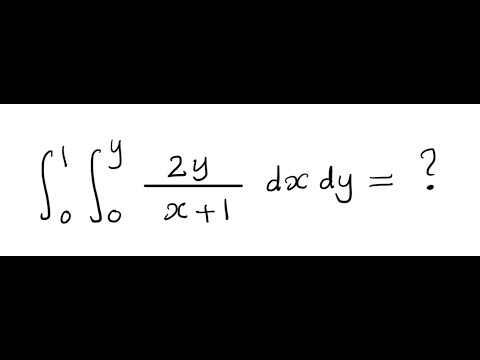 0:10:24
0:10:24
 0:10:05
0:10:05