filmov
tv
Finding the sum of ln(n)/n , n=1 to infinity
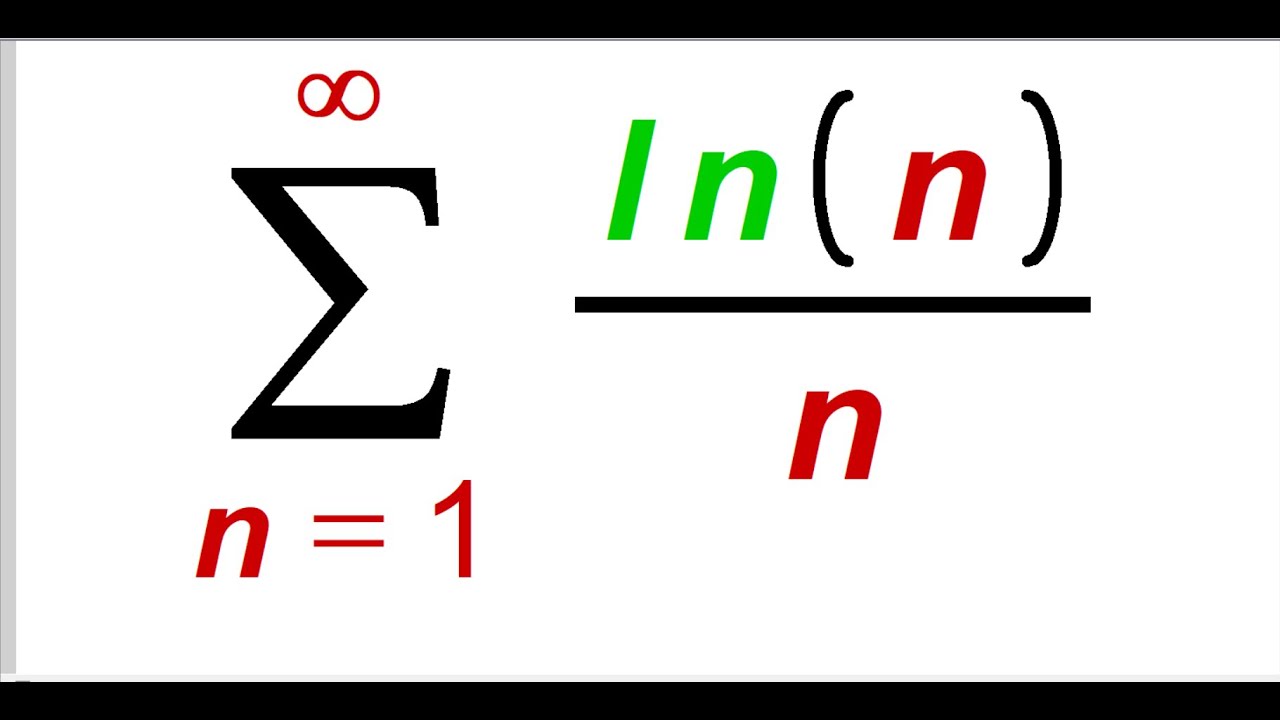
Показать описание
Today, I will show you how to find the sum from N equals one to positive infinity of ln(n)/n. To begin, let f(x) be equal to ln(x)/x. We need to determine where f(x) starts to decrease. By taking the derivative of f(x), which is -ln(x+1)/x^2, we find that f'(x) is negative when ln(x+1)/x^2 is less than zero. Solving this inequality, we get ln(x) greater than 1, which leads to x greater than e. Since x is a discrete variable, we choose n to be 3, the smallest whole number greater than e.
Now, using the integral test, we evaluate the integral of ln(x)/x from 3 to infinity. By separating the integral as ln(x) * (1/x) dx, we let u = ln(x) and du = (1/x) dx. Substituting these values, the integral becomes ln(3) to infinity of u du. Applying the power rule to integrate, we get (1/2)u^2.
Since the upper limit is infinity, we take the limit as the upper limit approaches infinity. Plugging in ln(3) for u, we have (1/2)ln^2(3) as the final result. This tells us that the sum of ln(n)/n diverges when n is greater than or equal to 3.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
Now, using the integral test, we evaluate the integral of ln(x)/x from 3 to infinity. By separating the integral as ln(x) * (1/x) dx, we let u = ln(x) and du = (1/x) dx. Substituting these values, the integral becomes ln(3) to infinity of u du. Applying the power rule to integrate, we get (1/2)u^2.
Since the upper limit is infinity, we take the limit as the upper limit approaches infinity. Plugging in ln(3) for u, we have (1/2)ln^2(3) as the final result. This tells us that the sum of ln(n)/n diverges when n is greater than or equal to 3.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
 0:04:34
0:04:34
 0:01:40
0:01:40
 0:14:01
0:14:01
 0:01:52
0:01:52
 0:04:36
0:04:36
 0:02:37
0:02:37
 0:01:44
0:01:44
 0:01:25
0:01:25
 3:22:07
3:22:07
 0:02:03
0:02:03
 0:06:31
0:06:31
 0:04:04
0:04:04
 0:03:46
0:03:46
 0:00:49
0:00:49
 0:02:48
0:02:48
 0:03:58
0:03:58
 0:03:12
0:03:12
 0:08:50
0:08:50
 0:01:56
0:01:56
 0:03:43
0:03:43
 0:01:16
0:01:16
 0:02:48
0:02:48
 0:01:13
0:01:13
 0:06:42
0:06:42