filmov
tv
The three-fold symmetry of chromogeometry | Rational Geometry Math Foundations 141 | NJ Wildberger

Показать описание
There are three planar metrical geometries that fit together beautifully; the usual Euclidean geometry (which we call blue), and two relativistic geometries (red and green). Most of the fundamental theorems of the subject hold for all three. But even more remarkably, when we transcend Klein's Erlangen program and consider all three geometries simultaneously, many completely new and unexpected relations and patterns appear.
This is a key door into 21st century geometry. Hundreds of fascinating discoveries await those who venture forth and learn how to think about geometry in this bigger, richer way. It also provides a lot of evidence to support the purely algebraic, logical point of view that results from letting go of the `real number' dreaming!
Video Content:
00:00 Intro to chromogeometry!
2:23 The green relativistic structure
6:28 Projective line
8:43 Exercises
11:10 Blue, red and green quadrances
12:45 Coloured quadrances theorem
15:31 Perpendicularity
17:46 Relation between three perpendiculars
***********************
Here are the Insights into Mathematics Playlists:
This is a key door into 21st century geometry. Hundreds of fascinating discoveries await those who venture forth and learn how to think about geometry in this bigger, richer way. It also provides a lot of evidence to support the purely algebraic, logical point of view that results from letting go of the `real number' dreaming!
Video Content:
00:00 Intro to chromogeometry!
2:23 The green relativistic structure
6:28 Projective line
8:43 Exercises
11:10 Blue, red and green quadrances
12:45 Coloured quadrances theorem
15:31 Perpendicularity
17:46 Relation between three perpendiculars
***********************
Here are the Insights into Mathematics Playlists:
The three-fold symmetry of chromogeometry | Rational Geometry Math Foundations 141 | NJ Wildberger
An introduction to chromogeometry | WildTrig: Intro to Rational Trigonometry | N J Wildberger
Chromogeometry and the Omega triangle | WildTrig: Intro to Rational Trigonometry | N J Wildberger
How Chromogeometry transcends Klein's Erlangen Program for Planar Geometries| N J Wildberger
Rational trigonometry, generalized triangle geometry and four-fold incenter symmetry
Proofs in chromogeometry | WildTrig: Intro to Rational Trigonometry | N J Wildberger
Chromogeometry and Euler lines | WildTrig: Intro to Rational Trigonometry | N J Wildberger
Spreads, determinants and chromogeometry (II) | WildTrig: Intro to Rational Trigonometry
Chromogeometry and nine-point circles | WildTrig: Intro to Rational Trigonometry | N J Wildberger
Spreads, determinants and chromogeometry (III) | WildTrig: Intro to Rational Trigonometry
Spreads, determinants and chromogeometry (I) | WildTrig: Intro to Rational Trigonometry
How To Draw 3-Fold Symmetry | Waldorf Geometry Tutorial
The chromatic algebra of 2x2 matrices I | Wild Linear Algebra B 41 | NJ Wildberger
The chromatic algebra of 2x2 matrices II | Wild Linear Algebra B 42 | NJ Wildberger
Seminar: Five-fold symmetry, Schiffler points and the twisted icosahedron
Geometry with a general dot product | WildTrig: Intro to Rational Trigonometry | N J Wildberger
Relativistic dot products and complex numbers | Wild Linear Algebra B 40 | NJ Wildberger
Sara Negri – A three-fold method for non-classical logics
Become a Patron of `Insights into Mathematics'
Advice for prospective research mathematicians | Rational Trigonometry and spread polynomials 1
The Triple spread formula, circumcircles and curvature | Rational Geometry Math Foundations 146
Relativistic dot products and complex numbers II 40b | Wild Linear Algebra B | NJ Wildberger
Isometry groups of the projective line (I) | Rational Geometry Math Foundations 138 | NJ Wildberger
The Story of the Threefold Human
Комментарии
 0:09:41
0:09:41
 0:07:37
0:07:37
 0:47:41
0:47:41
 0:50:25
0:50:25
 0:09:58
0:09:58
 0:08:19
0:08:19
 0:20:26
0:20:26
 0:07:54
0:07:54
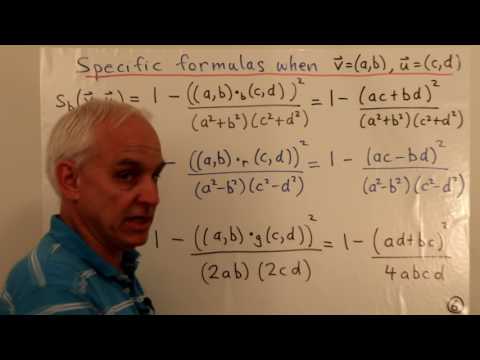 0:19:54
0:19:54
 0:19:26
0:19:26
 0:04:25
0:04:25
 0:32:14
0:32:14
 0:37:56
0:37:56
 0:51:55
0:51:55
 0:23:27
0:23:27
 0:38:06
0:38:06
 1:05:48
1:05:48
 0:01:25
0:01:25
 0:35:18
0:35:18
 0:23:58
0:23:58
 0:25:28
0:25:28
 0:34:26
0:34:26
 0:08:35
0:08:35