filmov
tv
y'' - 5y' + 6y = xe^x

Показать описание
Determine the particular solution to the given differential equation y'' - 5y' + 6y = xe^x. In other words, find the particular solution to the given non-homogenous differential equation using method of undetermined coefficients with characteristic/auxiliary equations and roots. y'' - 5y' + 6y = x*e^x. d^2y/dx^2 - 5 dy/dx + 6y = xe^x. d^2y/dx^2 - 5dy/dx + 6y = xe^x.
Hey everyone, I hope you learned and understood the Differential Equations problem (Solving Non-Homogenous Differential Equations with Method of Undetermined Coefficients) a little better. Feel free to ask me any questions or give me suggestions in the comments below. If you enjoyed the video, please give it a thumbs up. Thanks!
Separable Equations, Integration examples, integral examples, antiderivative examples, differential equations, integral practice problems, calculus 1 practice problems, differential equations practice problems, initial value problem, approximate solution, characteristic equations, auxiliary equations, roots, root solutions, complex roots, method of undetermined coefficients. James Stewart Single Variable Calculus. Nagle, Saff, Snider Fundamentals of Differential Equations. In Problems 9–26, find a particular solution to the differential equation. dy/dx. x*e^x. x*e^(x). xe^x.
This video is part of a comprehensive walkthrough of the most common problems you will run into during Differential Equations. I hope you find this playlist helpful!
Hey everyone, I hope you learned and understood the Differential Equations problem (Solving Non-Homogenous Differential Equations with Method of Undetermined Coefficients) a little better. Feel free to ask me any questions or give me suggestions in the comments below. If you enjoyed the video, please give it a thumbs up. Thanks!
Separable Equations, Integration examples, integral examples, antiderivative examples, differential equations, integral practice problems, calculus 1 practice problems, differential equations practice problems, initial value problem, approximate solution, characteristic equations, auxiliary equations, roots, root solutions, complex roots, method of undetermined coefficients. James Stewart Single Variable Calculus. Nagle, Saff, Snider Fundamentals of Differential Equations. In Problems 9–26, find a particular solution to the differential equation. dy/dx. x*e^x. x*e^(x). xe^x.
This video is part of a comprehensive walkthrough of the most common problems you will run into during Differential Equations. I hope you find this playlist helpful!
Комментарии
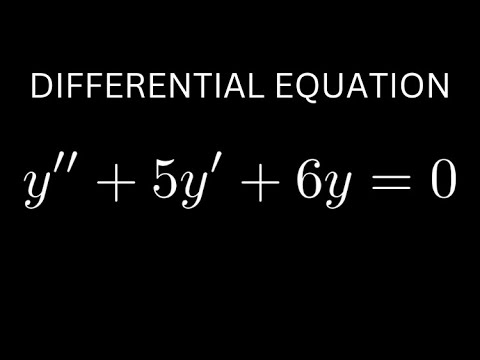 0:02:50
0:02:50
 0:04:26
0:04:26
 0:01:26
0:01:26
 0:01:06
0:01:06
 0:03:52
0:03:52
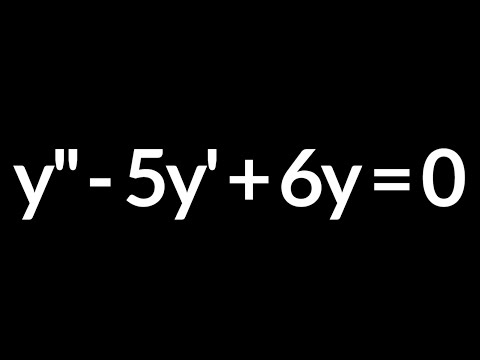 0:01:32
0:01:32
 0:01:57
0:01:57
 0:03:53
0:03:53
 0:02:43
0:02:43
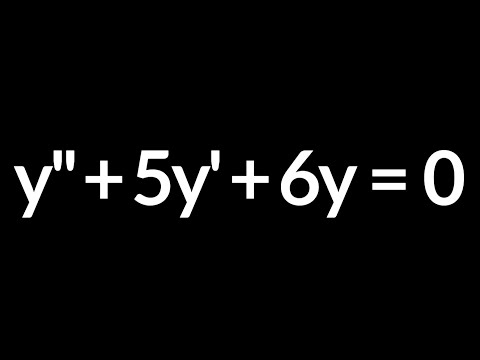 0:01:37
0:01:37
 0:03:31
0:03:31
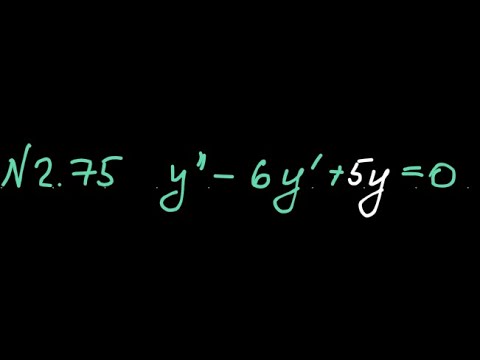 0:03:12
0:03:12
 0:00:15
0:00:15
 0:00:33
0:00:33
 0:01:01
0:01:01
 0:05:59
0:05:59
 0:08:21
0:08:21
 0:00:33
0:00:33
 0:01:18
0:01:18
 0:00:41
0:00:41
 0:07:46
0:07:46
 0:06:18
0:06:18
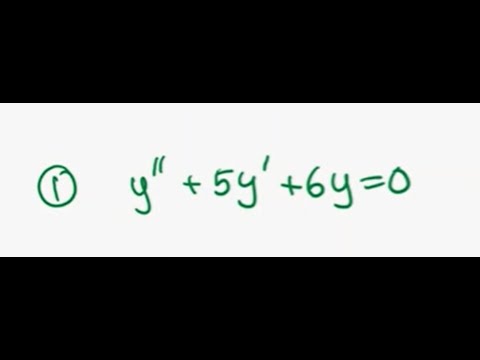 0:01:53
0:01:53
 0:14:59
0:14:59