filmov
tv
Wiskunde - Parallax-methode - afstand tot een ster bepalen

Показать описание
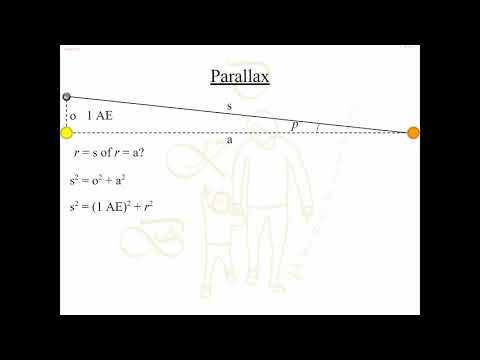
Een makkelijke? manier om te berekenen hoe ver een ster van de aarde/zon af staat is de parallax-methode.
parallax methode
Wiskunde - Parallax-methode - afstand tot een ster bepalen
Wiskunde - Parallax-methode
Parallax formule
V13 video 3 Parallax-methode
Astrofysica - Parallax
Stellar Parallax - IB Physics
Parallaxe
Measuring distances to stars (Stellar Parallax - Detailed Explanation)
Parallax method of measuring distance to stars
PARALLAX Method | An Activity-Based Explanation | How to measure distances of Stars and Planet?
Afstanden in het heelal (parallaxmethode = geen examenstof, rest van de video wel)
Wiskunde D op afstand - Hub Kusters
Natuurkundeles 13.3 Stralingsvermogen en afstand van sterren
Easy problems to understand parallax method
Rekenen met de lichtsnelheid - Tijd, afstand en snelheid (havo/vwo A/C) - WiskundeAcademie
Afstand van een ster tot aarde m.b.v. Herzsprung-Russeldiagram
Parallax uitleg
Assertion : Parallax method cannot be used for measuring distance of stars morer then 100
What is Parsec ? How 1 parsec is measured?
The Ultimate Guide to Determining Star Distances: Methods Unveiled
Measurement of length,parallax method
PARALLAX -- how to measure distances using parallax methods
I.1. Einleitung Entfernungen und Parallaxenmethode
Комментарии
 0:05:41
0:05:41
 0:03:59
0:03:59
 0:12:33
0:12:33
 0:00:55
0:00:55
 0:06:21
0:06:21
 0:06:40
0:06:40
 0:12:28
0:12:28
 0:00:55
0:00:55
 0:05:38
0:05:38
 0:06:08
0:06:08
 0:13:01
0:13:01
 0:08:16
0:08:16
 0:01:05
0:01:05
 0:14:49
0:14:49
 0:07:14
0:07:14
 0:06:18
0:06:18
 0:06:16
0:06:16
 0:06:57
0:06:57
 0:03:01
0:03:01
 0:03:14
0:03:14
 0:15:55
0:15:55
 0:07:19
0:07:19
 0:52:48
0:52:48
 0:09:02
0:09:02