8 / The spacetime of special relativity

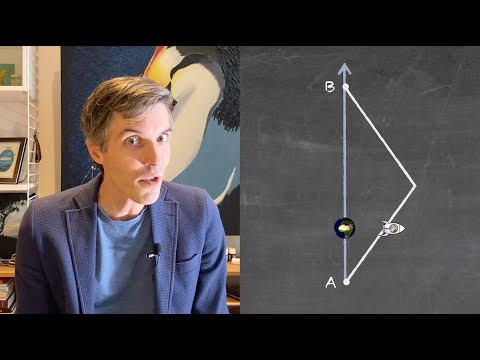
How the geometry of Minkowski spacetime and its tilting hypersurfaces of simultaneity allows one to visualise time dilation, length contraction, and the relativity of simultaneity in special relativity — with a little help from the Twin Problem (or Twin Paradox).

🍎️ Learn more about space, time and Einstein:

🍎️ Help more people learn about relativity theory:

🍎️ Designed, animated, created and produced in a living room by:
Dr Bryan W Roberts
Associate Professor, Philosopher of Physics, and Director of the LSE Centre for Philosophy of Natural and Social Sciences

[jasondarrenmandel]

Professor- really appreciate your work here! Reading Einstein’s papers requires work like yours to more fully grasp the concepts. Thank you.

[richardhinojos]

Thoughtfully explained in ways digestible by just about anyone! Dr. Roberts, thanks for this exceptional series. I will do my part to draw more attention and views to your work here. Please keep up the posts! They are greatly appreciated.

[frankmccoy]

Looks excellent for anyone because relativity is difficult for everyone. I will study this and see if it works for me. I have been watching everyone from Brian Greene to Sabine, to 10 others. Some are not well done, some not. I'm still working hard to get the concepts of relativity. You also do not demand much math which might help many. Getting these unusual concepts must start with many, without heavy math. Math folks can start with that but many of us need the concepts first, then we can go for the math if we want. Some don't have the math. I have enough math through calculus but one only needs algebra. So I will go back over the math once I get the strange concepts fixed in my mind. One certainly needs to keep the postulates of SR in mind constantly. So thanks and Keep up the good work.

[ObiektR]

Thanks for your work on all these videos, some of the clearest explanations I've seen!

[temptemp-eq]

So relativity prove that running is good for your life since who is in more motion is aging slower, and also proving that when you just do nothing it is really takes much longer.

[louismccartan]

What does this mean for our relationships on earth what does it mean if my wife is driving away from. Does her perception not exist for me?

[physicsVischi]

There is a type of Space-Time diagram in which the scale for both systems is the same. They are called "Loedel Palumbo Diagrams" and with them any analysis of special relativity is significantly simpler. They were developed in the mid-20th century by the Uruguayan physicist Enrique Loedel Palumbo from the simple, but brilliant idea, of considering in a diagram of Minkowski not one, but two "mobile" systems with the same speed, but in opposite directions and then remove the "fixed" system from the middle and... voila! you have two systems with the same scale! .The relative speed between these two systems is now given by the sine of the angle between the axes, not by the tangetic and trigonometry is that of all life. It is a shame that they are not very widespread.The deduction is very simple and can be found in the following link

[massimilianodellaguzzo]

If we accept Minkowski's space-time, a great contradiction is generated:
1) if we consider the frame of the Earth at rest, the astronaut twin's clock slows down,
2) if we consider the frame of the spaceship at rest, the Earth's clock slows down.

This is a contradiction, a great contradiction, and in my opinion no mathematics can justify it.

The astronaut twin moves in the frame of the Earth at speed v and it is not possible to imagine the Earth moving at the same speed (speed - v) in the frame of the spaceship. If so, two distances would be in relative motion between them and the twins would be the same age. The Earth-star distance contracts for the astronaut twin, while for the Earth no distance is contracted. (otherwise the twins would be the same age, it makes no sense to imagine the twin on Earth younger)
If two distances are in relative motion to each other, the distances overlap and neither of the twins would be younger than the other twin, I think the twin paradox is not a real paradox. (and it is possible to prove this using the Lorentz Transformations)

The spaceship actually moves with uniform rectilinear motion between any two points of the Earth’s frame (if the acceleration of the spaceship is zero). The astronaut twin leaves from the Earth to reach a star, the Earth and the star belong to the frame of the Earth! (all the other points reached by the spaceship also belong to the frame of the Earth)
All experiments confirm that moving objects are younger. (and I am thinking of atmospheric muons for example)

The spaceship's clock slows down relative to the Earth's clock, and the reverse cannot be true.