filmov
tv
Using Definite Integral Properties
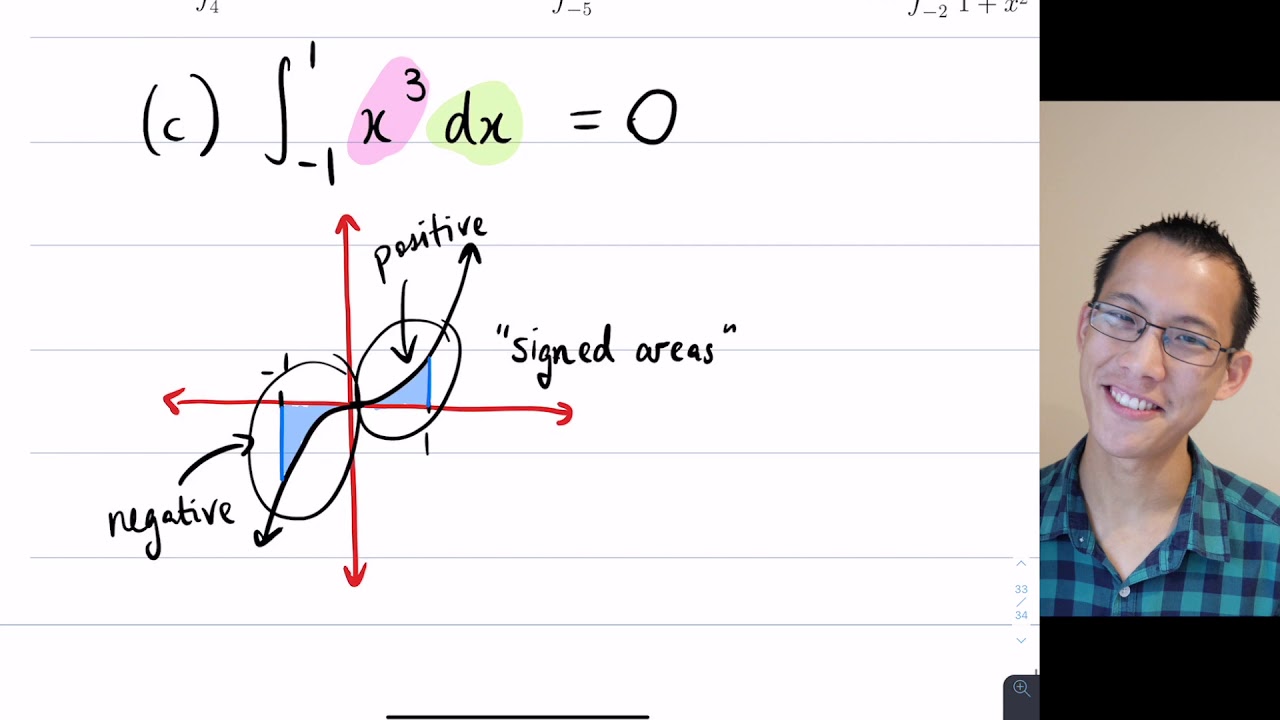
Показать описание
Using Definite Integral Properties
Properties of Integrals and Evaluating Definite Integrals
Definite Integral
Worked examples: Definite integral properties 1 | AP Calculus AB | Khan Academy
Definite integral properties (no graph): function combination | AP Calculus AB | Khan Academy
Properties of The Definite Integral
Calculus 1 Lecture 4.4: The Evaluation of Definite Integrals
Trick to Remember Definite Integral Properties / Don't Memorize
Evaluating the definite integral using standard techniques
Definite integral properties (no graph): breaking interval | AP Calculus AB | Khan Academy
How to evaluate the integral given different integrands
Worked examples: Definite integral properties 2 | AP Calculus AB | Khan Academy
Ex: Properties of Definite Integrals - Difference and Sum of Definite Integrals
Finding definite integrals using area formulas | AP Calculus AB | Khan Academy
MOST IMPORTANT DEFINITE INTEGRAL PROPERTIES and how to use them | Jake's Math Lessons
King Rule of Definite Integrals | Manim Animations |
Finding The Area Under The Curve Using Definite Integrals - Calculus
Screencast 4.3.3: Evaluating definite integrals using integral properties
6.. Properties of Definite Integrals | Integration | Class 12 Maths
Comparison Properties of the Integral—Inequalities with Integrals | Math with Professor V
Evaluating Indefinite Integrals
USING THE DEFINITE INTEGRAL PROPERTIES TO ADD INTEGRALS | Write as a single integral in the form
Evaluating Definite Integrals Using Geometry
A Peculiar Property of Definite Integrals // The King Rule (The Art of Integration)
Комментарии
 0:13:54
0:13:54
 0:09:48
0:09:48
 0:11:05
0:11:05
 0:02:18
0:02:18
 0:03:14
0:03:14
 0:07:46
0:07:46
 0:30:55
0:30:55
 0:11:24
0:11:24
 0:03:08
0:03:08
 0:04:32
0:04:32
 0:09:22
0:09:22
 0:05:26
0:05:26
 0:02:57
0:02:57
 0:04:17
0:04:17
 0:09:45
0:09:45
 0:05:12
0:05:12
 0:34:24
0:34:24
 0:08:15
0:08:15
 0:30:17
0:30:17
 0:35:03
0:35:03
 0:10:44
0:10:44
 0:04:02
0:04:02
 0:17:29
0:17:29
 0:21:26
0:21:26