filmov
tv
A Math Olympiad exponential math problem| solve for x,y.
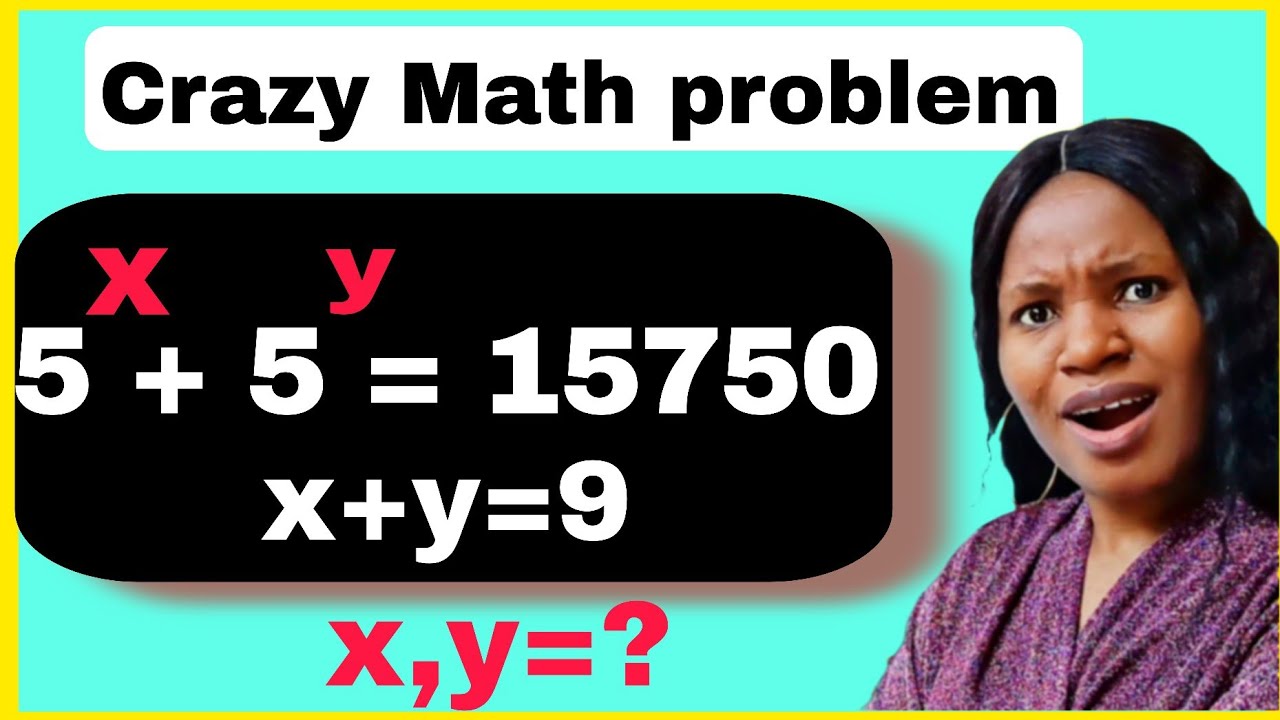
Показать описание
This is a tricky Math Olympiad exponential math question. #exponentialequationproblems #math
Always anticipate for my videos around 9 am and 9 pm WAT
Always anticipate for my videos around 9 am and 9 pm WAT
Germany | A nice Math Olympiad Exponential Simplification | You Should Master this Trick | #maths
A nice exponential equation to solve| Math Olympiad #maths #matheolympiad
Germany| Can you solve this? | A math Olympiad exponential problem
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Mexico - A Nice Math Olympiad Exponential Problem
United Kingdom - A Nice Exponential Equation | Math olympiad Question
A Nice Math Olympiad Exponential Equation 3^x = X^9
Korean Math Olympiad Question | A Nice Exponential Problem
China | Math Olympiad Exponential Challenge | A Nice Algebra Problem 👇👇👇
Germany - Math olympiad exponential problem | Find value x
A nice math olympiad exponential problem | Olympiad mathematics (x)=?
Math Olympiad|Exponential equation.
Germany | Can you solve this ?| A Nice Math Olympiad Exponential Problem
Japanese Math Olympiad Problem | A Nice Math Problem : Comparison
Français | Can you solve this ? | A nice Math Olympiad Exponential Simplification | Algebra Problem
Germany | A nice Logarithmic Math Olympiad Problem | Exponential Equation x^log27+3^logx=36 | x=?
A nice Math Olympiad Radical Simplification | Exponential Problem | #maths #matholympiad #exponents
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Français | Can you solve this ? | Math Olympiad Exponential Simplification | A nice Algebra Problem
Norway Math Olympiad Question | A Nice Exponential Question
Germany - Math Olympiad Exponential Problem.
A nice math olympiad exponential problem | Olympiad mathematics (x)=?
Germany | Exponential equation solving | Math olympiad equation
Nice Math Olympiad Simplification Problem | Fraction Exponents | You Should NOT use Calculators
Комментарии
 0:08:46
0:08:46
 0:04:55
0:04:55
 0:13:32
0:13:32
 0:00:52
0:00:52
 0:08:36
0:08:36
 0:09:19
0:09:19
 0:02:34
0:02:34
 0:03:15
0:03:15
 0:10:07
0:10:07
 0:02:20
0:02:20
 0:01:42
0:01:42
 0:03:40
0:03:40
 0:09:20
0:09:20
 0:04:15
0:04:15
 0:10:49
0:10:49
 0:12:15
0:12:15
 0:11:26
0:11:26
 0:10:49
0:10:49
 0:10:48
0:10:48
 0:02:28
0:02:28
 0:04:45
0:04:45
 0:01:40
0:01:40
 0:11:43
0:11:43
 0:13:59
0:13:59