filmov
tv
Prove the AM-GM Inequality: (a1 + a2 + ... + an)/n ≥ (a1a2...an)^1/n First Proof [ILIEKMATHPHYSICS]

Показать описание
This video is part of the "Intro to Higher Math" series I am making; it mainly references Daniel Velleman's book "How to Prove it" Third Edition. The exercise in this video is given by Exercise 8 of Section 6.2. The way the proof is done in this video is essentially the way it is guided in the exercise.
Also, every time we mention "list of length N" in the video, we mean "list of positive real numbers of length N".
There are many proofs on this; I am planning on making a video in the future giving another proof.
Thanks and enjoy the video!
Also, every time we mention "list of length N" in the video, we mean "list of positive real numbers of length N".
There are many proofs on this; I am planning on making a video in the future giving another proof.
Thanks and enjoy the video!
Prove the AM-GM Inequality: (a1 + a2 + ... + an)/n ≥ (a1a2...an)^1/n First Proof [ILIEKMATHPHYSICS]...
Prove the AM-GM Inequality: (a1 + a2 + ... + an)/n ≥ (a1a2...an)^1/n Third Proof [ILIEKMATHPHYSICS]...
Prove the AM-GM Inequality (a1 + a2 + ... + an)/n ≥ (a1a2...an)^1/n Second Proof
Let's Prove The AM-GM Inequality
Proving the Arithmetic Geometric Mean inequality (Am - Gm proof) with induction
Wonderful proof AM - GM inequality | Maths Olympiad Concept video
How to Prove AM-GM-LM Inequality on a 1/x graph
Proving the AM-GM Inequality with ZERO Calculus
Proof of the AM -GM inequaliy
Ext2 Inequalities: Elegant Proof of the AM-GM for n variables
Proof of AM-GM Inequality. Leap Forward Fall Back Induction.
The AM-GM Inequality by Luke Robitaille
Inequalities Tutorial #1 - Intro to AM-GM
The AM-GM Inequality - Problem
Proving AM-GM inequality
AM - GM Inequality - Elegant proof Part 2, the induction argument
A Mean Theorem! Proving the AM-GM-HM Inequalities Elegantly!
Math Olympiad Problem | AM-GM Inequality | an example
Euler Number and AM GM Inequality - Stories in Real Analysis
What Can We Learn From This RMO 1991 Problem 1 ? - AM - GM Inequality | IOQM, ISI-CMI Entrance, RMO
AM-GM Inequality | Arithmetic Mean Geometric Mean Inequality
Arithmetic geometric mean inequality
The AM-GM Inequality
Geometry of AM GM Inequality
Комментарии
 0:22:13
0:22:13
 0:14:16
0:14:16
 0:05:16
0:05:16
 0:09:44
0:09:44
 0:19:11
0:19:11
 0:10:22
0:10:22
 0:02:24
0:02:24
 0:09:22
0:09:22
 0:08:38
0:08:38
 0:19:14
0:19:14
 0:30:02
0:30:02
 0:08:29
0:08:29
 0:36:16
0:36:16
 0:06:43
0:06:43
 0:09:37
0:09:37
 0:09:26
0:09:26
 0:26:07
0:26:07
 0:04:38
0:04:38
 0:12:05
0:12:05
 0:13:09
0:13:09
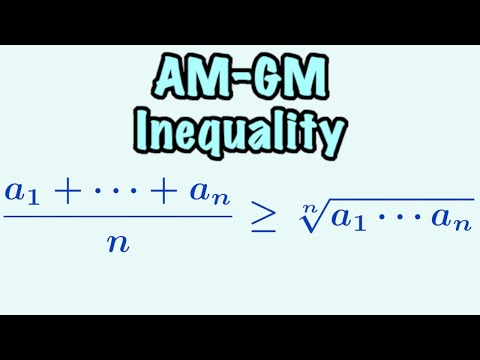 0:12:45
0:12:45
 0:17:18
0:17:18
 0:05:23
0:05:23
 0:08:46
0:08:46