Coin rotation paradox

The coin rotation paradox

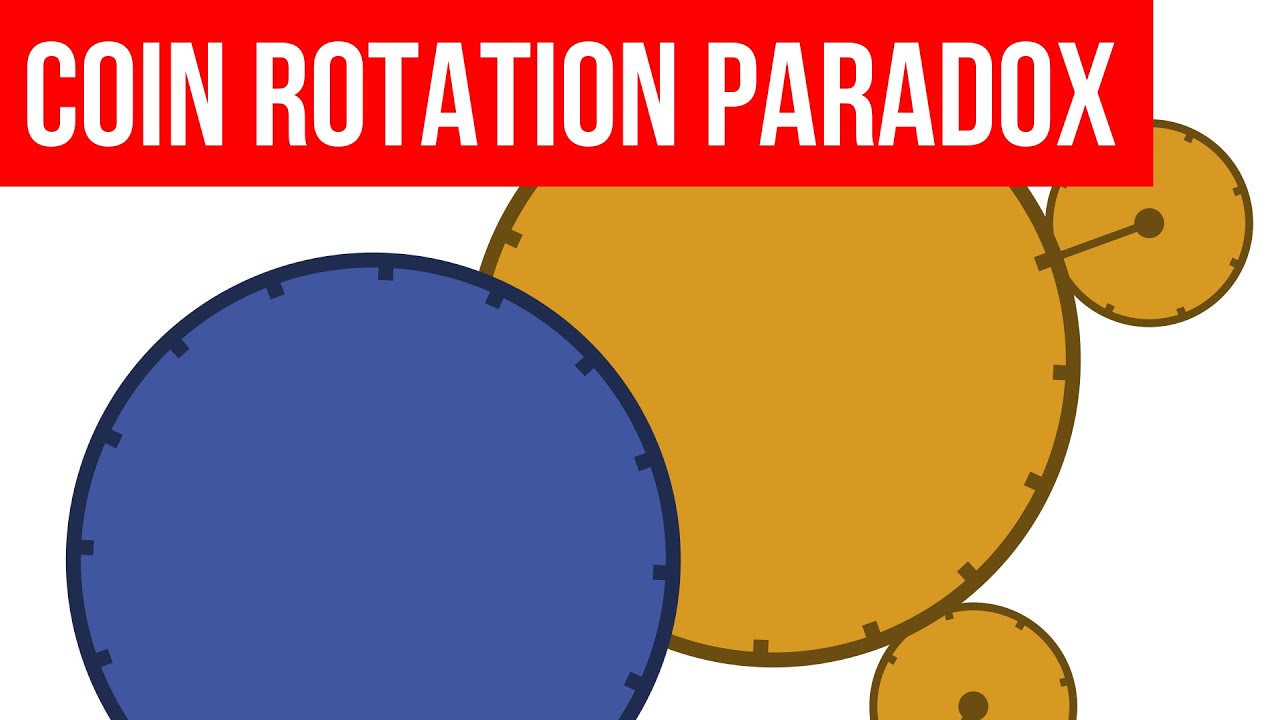
Imagine we have 2 coins. The radius of the larger coin is 3 times the radius of the smaller coin. We roll the smaller coin all the way around the edge of the larger coin, without it slipping.

The question is, how many times will the smaller coin rotate as it rolls around the edge of the larger coin?

The result is quite surprising, and this video explains why.

Related articles:

Links:

[dubzy]

This finally expalined it in a way i can get it. It's really been bugging me

[chrisg]

Lovely and clear. A couple of interesting variations: 1) the small circle does one less rotation when rolling round the inside edge of the big one. One consequence is that when the two circles are equal then the "inside" one can't roll, it does 1 - 1 = 0 rotations. 2) You can also have a small square rolling round a big one .

[Forestdogg]

What if we count the rotation if the marker is down AND actually touching the bigger circle

[arjitgupta]

You are the first one to explain this correctly in the best way ❤thank you. Stay on the ways, god is with you 😊

[akshayrao]

Some measure theory assumptions are hidden here in definition of coin moving without slipping.