Bounded Sequences and Sets in a Metric Space | Metric Spaces | Introduction to Real Analysis

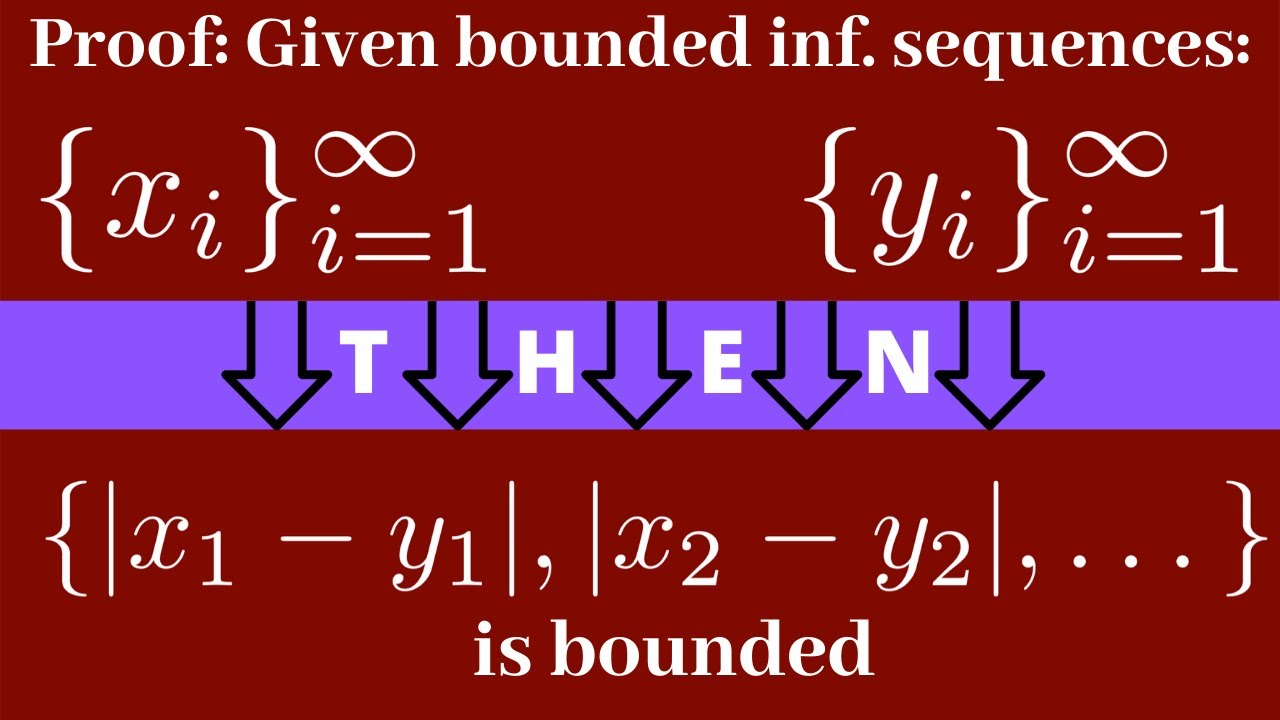
This video proves that if x = (x_1,x_2,...) and y=(y_1,y_2,...) are bounded infinite sequences, then the set {|x_1-y_1|, |x_2-y_2|, |x_3-y_3|,...} is bounded.

Proof: Bounded Sets Can Be Contained In Open or Closed Balls Centered Anywhere in a Metric Space

Proof that if (a-b) is less than epsilon and (b-a) is less than epsilon then |a-b| is less than epsilon:

Proof of: "a" less than "b" and "c" less than or equal to "d" implies (a+c) is strictly less than (b+d):

[maxpercer]

this video seems out of order in the playlist. but great video !