filmov
tv
Calculus 1: Limits & Derivatives (24 of 27) Finding the Limits of a Function - Example 11
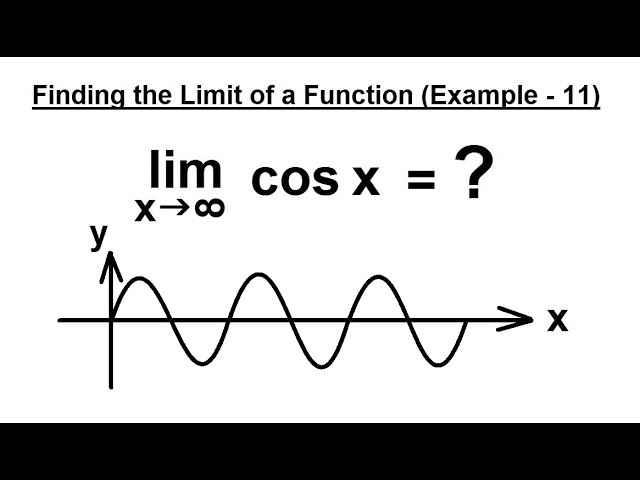
Показать описание
In this video I will calculate the limit(x approaches infinity) of cos(x).
Next video in the series can be seen at:
Calculus 1 - Introduction to Limits
Limits and Derivatives
Understand Calculus in 35 Minutes
Calculus 1 - Derivatives
Calculus - Finding the derivative of a function using limits
Visual Derivative Definition!
Introduction to limits | Limits | Differential Calculus | Khan Academy
Definition of the Derivative
Determine if the sum from n=1 to infinity of n/ln(n) converges or diverges #maths #calculus #series
3 WAYS TO SOLVE LIMITS
Limits and Limit Laws in Calculus
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
A tricky derivative using the limit definition #calculus
Calculus 1 Overview, (the connection between limit, derivative & integral)
recognize limits as derivatives, calculus 1 homework help
Limits and Continuity
Calculus 1: Limits & Derivatives (1 of 27) The Tangent Line and The Secant Line - Reviewed
Limits of functions | Calculus
Intro to Derivatives, Limits & Tangent Lines in Calculus | Step-by-Step
The paradox of the derivative | Chapter 2, Essence of calculus
What is a Limit - What is a Derivative , Calculus 1 , Lesson 1
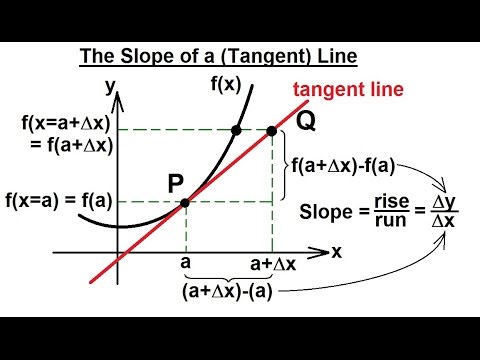
Calculus 1: Limits & Derivatives (2 of 27) The Slope of a Line
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
Calculus in a nutshell
Комментарии
 0:20:20
0:20:20
 0:05:23
0:05:23
 0:36:22
0:36:22
 0:52:51
0:52:51
 0:04:36
0:04:36
 0:01:00
0:01:00
 0:11:32
0:11:32
 0:23:31
0:23:31
 0:00:48
0:00:48
 0:05:00
0:05:00
 0:12:49
0:12:49
 0:18:27
0:18:27
 0:00:38
0:00:38
 0:10:33
0:10:33
 0:08:50
0:08:50
 0:19:19
0:19:19
 0:02:06
0:02:06
 0:15:09
0:15:09
 0:28:33
0:28:33
 0:16:50
0:16:50
 0:04:40
0:04:40
 0:07:00
0:07:00
 0:07:16
0:07:16
 0:03:01
0:03:01