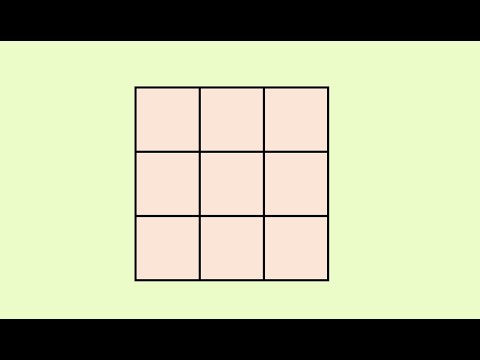
How many squares are in different sizes of grids? #shorts

#shorts #short #math #mathematics #squares #grid #square #puzzle #formula #pattern

Combo Class is a crazy educational show where you can have fun learning rare things about math, science, language, and more! This is the SHORTS channel for faster-paced videos. Make sure you're also subscribed to the main Combo Class channel where full episodes go!

DISCLAIMER: any use of fire, tools, or other science experiments in this series is always done in a safe and professional way. Do not try to copy any actions you see in this series yourself.

[Domotro]

Check out this longer new video I made with this topic expanded to more shapes like rectangles and triangles:

[neelsharma]

him: how many squares are in this picture.
me: four
him: you might be able to count there's five
me : ...

[inferno]

Learning math from a guy crouched under a tree

[bappibhai]

Math rule 101:
Never try to come up with the solution
Come up with a formula

[nanakiblox]

Me walking in the woods when a man comes out of a bush and says "how many squares are in this picture"

[victorokah]

"Honey jack harlow is in our backyard teaching the kids math again"

[kimtgf]

I actually discovered (might be a big word but It was the first time for me) this formula some 2 years back when I had a question on an exam on how many squares are in a chessboard, I found this same type of recursion and left feeling like an absolute champ.

[georgiolegaci]

Bro looks like Hans Niemann an Jack Harlow combined

[JoshZnh]

"Sir, what are you doing on my backyard"

[alankritbansal]

Number of parellolograms in a parallelogram formula:

Rows addition × column addition

Since square is a type of parallelogram and rectangle too (they satisfy property of parallelogram: opposite side being parallel)

Number of rectangles in the last 6×6 square is:

(1+2+3+4+5+6)×(1+2+3+4+5+6)= 21×21=441 rectangles

A topic of permutations and combination.

9th grade in Kota, education capital of
India 🇮🇳 as many students come to Kota to prepare for exams like iit jee, neet.

[xrekshot]

Him: (calling over kids that are alone under a tree) Hey kid want free math advice

[arienmartinez]

Do I counted and there seems to be 91:
36 - 1*1
25 - 2*2
16 - 3*3
9 - 4*4
2 - 5*5
1 - 6*6

[nicholasboffa]

I think there was a 3b1b video on the rectangle problem? The trick is to start thinking in terms of 'choosing' 2 out of n lines to be one set of the rectangle's sides, and then choosing another 2 the same way using combinatorics.

[TutorJeff]

You actually manage to make something boring like this super fun. Your presentation is flawless. As a scientist, I can feel just how much fun you are having while presenting. I loved your video on 1/0 too

[sanju.meshram]

Feels soo good when you get it right!! :D
Its 91!

[Lalo-Salamanca.]

Jack Harlow using his brain for 3 seconds :

[FizzyK-]

I love the way he said "Square Numbers" 😂

[boazburger]

I figured this out on my own, and was like: "wait... Am i smart?" But then I tried to eat a coin instead of a tosti.

[AndraRill]

I think the Formula is
Total length of the biggest square -> n
n² + (n-1)² + (n-1-1)² ... and goes on until the n reaches "1"

Correct me if im wrong

[nanamacapagal]

Challenge accepted!

Black Pen Red Pen actually talked about this problem before (the rectangle one) so my solution would be very similar

Each rectangle has a length and a width. Let's separate them and try choosing the length first

I'll go for a concrete example but I'll also build a general case

Say I have 6 rows of squares in the grid, and I have to choose which rows to include in my rectangle. There's 6 ways to pick 1 row, 5 ways to pick 2 (because you can't have gaps), 4 ways to pick 3, and so on. That's 6+5+4+3+2+1 which is the 6th triangular number which is 21.

And in general if you have M rows in the grid, the total number of ways to pick the rows is the Mth triangular number or M(M+1)/2.

Now there's nothing special about me using rows. I can play the same argument but with 6 columns (N columns). Better, whatever I chose for M does not restrict me in what I can choose for N. I can even have a different number of columns than rows in the starting GRID and the argument still makes sense.

So the total number of rectangles in a 6x6 grid is 6(7)/2 * 6(7)/2 = 441. In a 6x7 grid it's 6(7)/2 * 7(8)/2 = 588. And in an MxN grid it's M(M+1)/2 * N(N+1)/2.

Again, there's nothing special with using 2 dimensions for this argument, so the number of rectangular prisms is just M(M+1)/2 * N(N+1)/2 * O(O+1)/2. And in D dimensions, it's the product of M(M+1)/2, where M is the number of squares in the row/column/whatever orthogonal direction for all orthogonal directions that make up D.

The square argument YOU showed also generalizes to squares in a rectangle and cubes in a rectangular prism

For an MxN grid (4x6 as an example, WLOG I will assume M is less than or equal to N), the largest square you can make is MxM (4x4).

The number of 1x1 squares is MxN (4x6), the number of 2x2 squares is (M-1)(N-1) (3x5), and so on until you get to the number of MxM squares which is (1)(N-M+1) or just N-M+1 (1x3). The total is the sum of all of that, in our 4x6 example it's 4x6 + 3x5 + 2x4 + 1x3 = 50.

And in higher dimensions we can play the same game with cubes or hypercubes in rectangular prism grids. Just decrease every dimension by 1 until one of the dimensions hits 1, then multiply and add.

In a 4x5x6 rectangular prism there are 4x5x6 + 3x4x5 + 2x3x4 + 1x2x3 = 210 cubes inside.