If tan(α+iβ)=x+iy , prove that (i)x²+²y+2xcot2α=1(ii) x²+y²-2ycothy+1=0, (iii) x. cot2α+ycoth2β=1

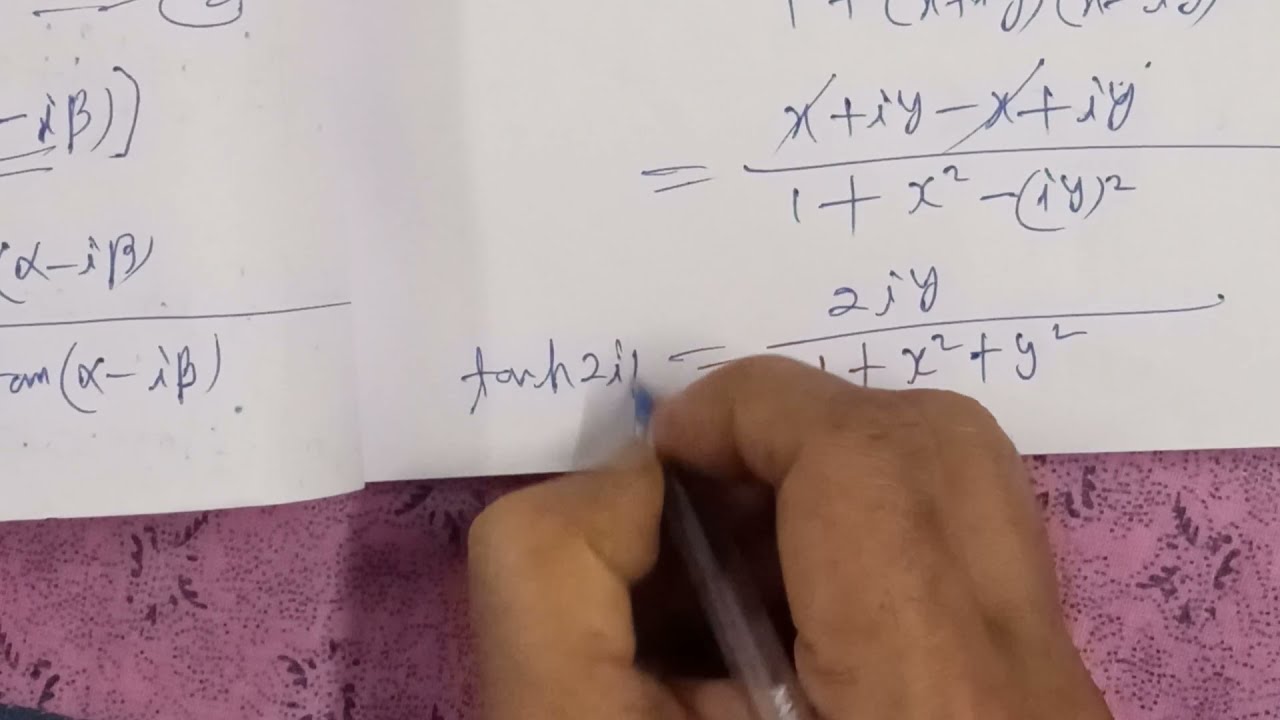
preview_player
Показать описание
If tan(α+iβ)=x+iy , prove that (i)x^2+y^2+2xcot2α=1(ii) x^2+y2-2ycothy+1=0, (iii) x. cot2α+ycoth2β=1
  1. Doctor of Mathematics
Рекомендации по теме
If tan(α+iβ)=x+iy , 0:08:44

If tan(α+iβ)=x+iy , prove that (i)x²+²y+2xcot2α=1(ii) x²+y²-2ycothy+1=0, (iii) x. cot2α+ycoth2β=1...

If tan(A+iB)=x+iy prove 0:10:55

If tan(A+iB)=x+iy prove that (1)tan2A=2x/1-x^2-y^2(2) tanh2B=2y/1+x^2+y^2

if tan(a+ib)=x+iy,then prove 0:04:31

if tan(a+ib)=x+iy,then prove that x²+y²-2ycoth2b+1=0| #trigonometry #bscmaths #ppu @mathhat19 #pyqs...

hyperbolic functions|problem 2 0:10:42

hyperbolic functions|problem 2

separate real and 0:07:54

separate real and imaginary parts of tan(x+iy)| hyperbolic functions

If x + 0:02:03

If x + iy = a + iba - ib prove that x^2 + y^2 = 1 Complex number 11th Maths

If x+iy = 0:15:41

If x+iy = tan(A+iB) prove that # Trigonometry # SM22A # April 2022 # Allied maths 1

if tan log 0:03:03

if tan log ( x+iy)=a+ib where a^2+b^2 not equal to 1. prove: tan log (x^2+y^2)= 2a/1-a^2-b^2..

if sin(A+iB)=x+iy and 0:03:12

if sin(A+iB)=x+iy and if A,B,x,y are real , prove that :- (x²/sin²A)-(y²/cos²A)=1 | #bscmaths #part1...

Maths BSc 2 0:18:33

Maths BSc 2 | Exercise 1.4 | Q.7 | if a^ (α +i β)= (x+ iy)^(p+iq) Complex Number

Examples on Hyperbolic 0:20:17

Examples on Hyperbolic functions! Part-2

If iⁱ⁻⁻⁻= α+iβ 0:10:05

If iⁱ⁻⁻⁻= α+iβ then prove that tan〈πα/2)=β/α and α²+β²=e^-πβ.

if A + 0:04:52

if A + iB = Ctan (x + iy), P.T. tan2x = 2AC /(C^2- A^2 -B^2) II B. Sc. maths II @h.emathematics7916

if tan(theta+iphi)=sin(x+iy) then 0:07:04

if tan(theta+iphi)=sin(x+iy) then show that coth y . sinh 2phi = cot x. sin 2theta @jaggi mathur

TRIGONOMETRY/HYPERPBOIC FUNCTION/EXAMPLE 4&5/KS 0:08:43

TRIGONOMETRY/HYPERPBOIC FUNCTION/EXAMPLE 4&5/KS UG MATHS/TAMIL

TRIGONOMETRY/HYPERPBOIC FUNCTION/EXAMPLE 6&7/BSC 0:11:41

TRIGONOMETRY/HYPERPBOIC FUNCTION/EXAMPLE 6&7/BSC MATHEMATICS/KS UG MATHS

if tanh(u+iv)=sin(x+iy),prove that 0:09:18

if tanh(u+iv)=sin(x+iy),prove that sinh2u/sin2v=tanx/tanhy| Trigonometry important Question & An...

x+iy = a+ib/a-ib 0:05:56

x+iy = a+ib/a-ib then prove that x²+y² = 1

Real and imaginary 0:04:12

Real and imaginary part of tan inverse of x+iy//GBK maths//Gate//M1//NET//SET//B.Sc //M2//

separate into real 0:03:05

separate into real and imaginary part tan inverse x+iy ||Function of complex variable @visibleyt

If tan(x+iy)=cos@+isin@,then prove 0:13:23

If tan(x+iy)=cos@+isin@,then prove that e^2y=tan[pi/4+@/2]

If x + 0:05:23

If x + iy = (a + ib)/(a - ib) Prove that x² + y² = 1

Prove: If |cos(x+iy)| 0:08:37

Prove: If |cos(x+iy)| = 1 or cos⁡(x+iy)= cosa + isina, then prove cos2x+cosh2x=1

if sin(x+iy)=r(cos@+isin@),prove that 0:07:12

if sin(x+iy)=r(cos@+isin@),prove that (i) tan@=tanhy.cotx , (ii) 2r²=cosh2y-cos2x #bscmaths #ppu

Комментарии
Автор

chapter -Hyperbolic functions
Ques- If x+iy=c tanh (u+iv), where x, y, c, u and v are all real, prove that x^2 + y^2 + c^2 - 2cx coth 2u=0
Sir please solve my doubt as early as possible🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏🙏

Justfor_funn
Автор

heyy can u help im stuck on similar ques but couldnt find solution? if tan (x+y) = u+ iv then prove that u square +v square + 2ucot2x = 1

xen
Автор

Very less portion of your notebook's solution is visible on screen at a time, otherwise you are teaching good, sir.👍🏻

sonalisingh