Row Equivalence

Video Outline:
0:00 - 0:30 Review
0:30 Definition of Row Equivalence
1:34 Example of row equivalent matrices
1:45 Example part 1 - sequence of row operations transforming A into A'
2:19 Example part 2 - sequence of row operations transforming A' into A
4:31 Theorem
4:46 Lemma
4:57 Proof of Lemma
5:03 Proof of Lemma - part 1 (for the first row operation)
5:43 Proof of Lemma - part 2 (for the second row operation)
6:17 Proof of Lemma - part 3 (for the third row operation)
6:58 - 9:26 Proof of Theorem
9:35 Does the converse of the Theorem hold?
9:48 Counterexample for the converse of the theorem.

Important Definitions/Theorems:
Row Equivalence Definition: 2 matrices are row equivalent if there exists a sequence of elementary row operations transforming one matrix into the other.
Note: If 2 matrices A and B are row equivalent with some sequence transforming A into B, then there is also a sequence transforming B into A.
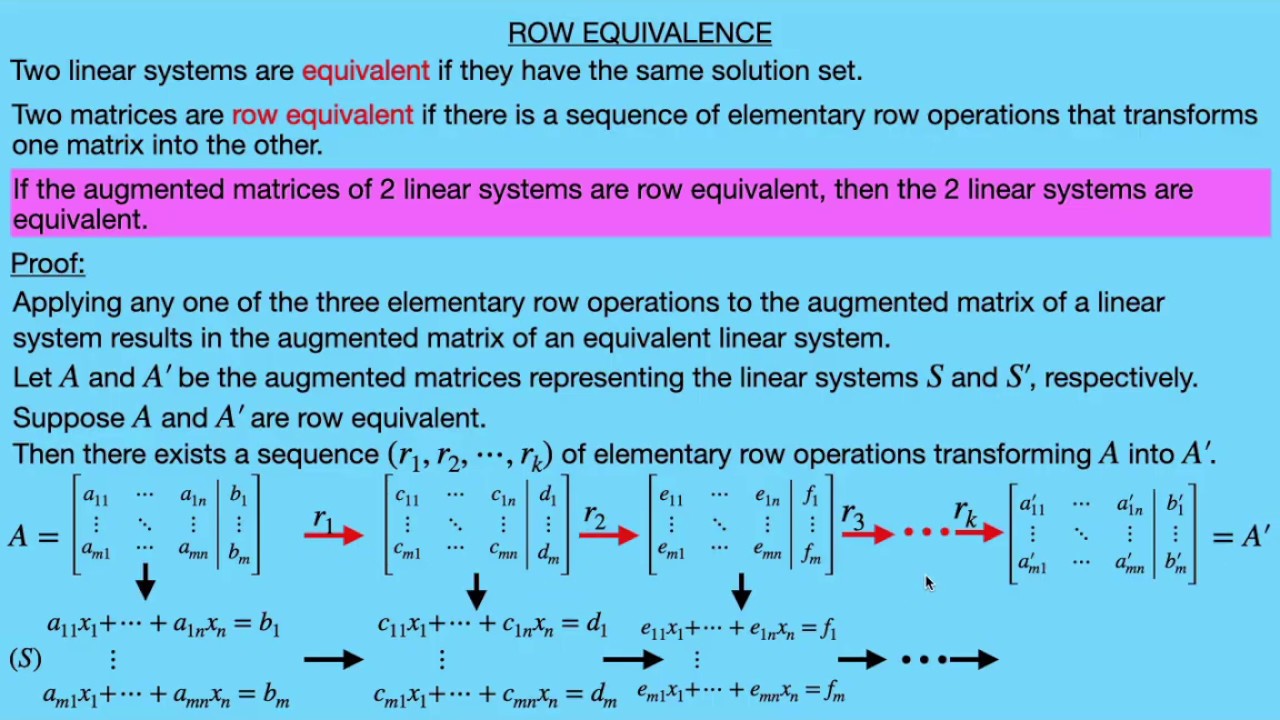
Theorem: If the augmented matrices of 2 linear systems are row equivalent, then the 2 linear systems are equivalent.
Lemma: Applying any one of the 3 elementary row operations to the augmented matrix of a linear system results in the augmented matrix of an equivalent linear system.